Mouvement d'une particule chargée dans un champ magnétique uniforme
Dans le cas d'un champ magnétique uniforme et en
l'abscence de champ électrique,
2 se simplifie

Ici, comme c'est simple, on peut traiter
directement le cas relativiste. En multipliant
2
par
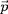
, on trouve que la variation d'énergie cinétique
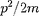
est nulle. Alors

est constant et
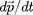
est orthogonal à
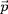
. De ce fait,

est constant. Alors

où
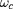
est une constante, la girofréquence définie par

On suppose que
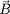
est parallèle à l'axe
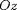
. En multipliant
4 par
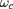
ou
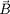
on voit que
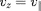
est constant. Dans le plan
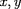
,


Les équations sur

ou

sont identiques : La solution est donc du type
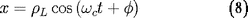
et comme
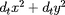
est constant,
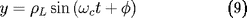
Le mouvement est circulaire de pulsation
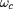
et de rayon
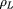
dans le plan perpendiculaire à la direction du
champ magnétique. On désignera dorénavant
par
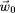
la vitesse (perpendiculaire à
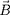
) que l'on peut déduire de
8,
9.
On appelle
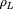
le rayon de Larmor (d'où la notation adoptée), on
peut le relier à la composante perpendiculaire de la
quantité de mouvement de la particule et d'autres
grandeurs de ce genre :
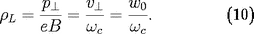
Il faut être conscient que dans le cas relativiste,
cette formule contient de l'information sur la
vitesse totale

qui est dans

, lui même caché dans

ou
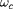
.
Dans le cas non relativiste, les résultats ci-dessus
demeurent, seulement on fait
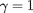
.
L'angle

entre la vitesse et le champ magnétique est appelé
l'angle d'attaque. On a
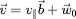
,
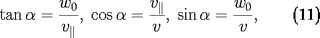
où
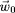
est la vitesse que l'on peut déduire de
8,
9.
L'
appliquette suivante permet de simuler le
mouvement d'une particule chargée dans un champ
uniforme (ici le mouvement calculé est non
relativiste).


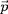 , on trouve que la variation d'énergie cinétique
, on trouve que la variation d'énergie cinétique
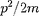 est nulle. Alors
est nulle. Alors
 est constant et
est constant et
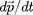 est orthogonal à
est orthogonal à
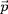 . De ce fait,
. De ce fait,
 est constant. Alors
est constant. Alors 
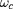 est une constante, la girofréquence définie par
est une constante, la girofréquence définie par

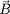 est parallèle à l'axe
est parallèle à l'axe
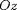 . En multipliant 4 par
. En multipliant 4 par
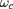 ou
ou
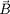 on voit que
on voit que
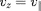 est constant. Dans le plan
est constant. Dans le plan
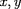 ,
, 

 ou
ou
 sont identiques : La solution est donc du type
sont identiques : La solution est donc du type
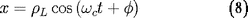
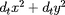 est constant,
est constant, 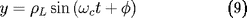
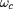 et de rayon
et de rayon
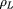 dans le plan perpendiculaire à la direction du
champ magnétique. On désignera dorénavant
par
dans le plan perpendiculaire à la direction du
champ magnétique. On désignera dorénavant
par
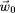 la vitesse (perpendiculaire à
la vitesse (perpendiculaire à
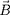 ) que l'on peut déduire de 8,9.
On appelle
) que l'on peut déduire de 8,9.
On appelle
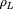 le rayon de Larmor (d'où la notation adoptée), on
peut le relier à la composante perpendiculaire de la
quantité de mouvement de la particule et d'autres
grandeurs de ce genre :
le rayon de Larmor (d'où la notation adoptée), on
peut le relier à la composante perpendiculaire de la
quantité de mouvement de la particule et d'autres
grandeurs de ce genre : 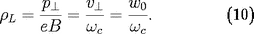
 qui est dans
qui est dans
 , lui même caché dans
, lui même caché dans
 ou
ou
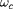 .
Dans le cas non relativiste, les résultats ci-dessus
demeurent, seulement on fait
.
Dans le cas non relativiste, les résultats ci-dessus
demeurent, seulement on fait
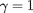 .
L'angle
.
L'angle
 entre la vitesse et le champ magnétique est appelé
l'angle d'attaque. On a
entre la vitesse et le champ magnétique est appelé
l'angle d'attaque. On a
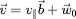 ,
, 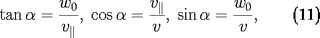
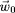 est la vitesse que l'on peut déduire de
8,9.
L'appliquette suivante permet de simuler le
mouvement d'une particule chargée dans un champ
uniforme (ici le mouvement calculé est non
relativiste).
est la vitesse que l'on peut déduire de
8,9.
L'appliquette suivante permet de simuler le
mouvement d'une particule chargée dans un champ
uniforme (ici le mouvement calculé est non
relativiste).