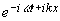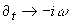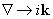Quelques éléments théoriques à propos des ondes d'Alfven
Laurence Rezeau
Date de mise à jour : 17/04/2002
Partant du système des
équations de la Magnéto-Hydro-Dynamique, on effectue les étapes suivantes (les calculs ne sont pas faits complètement, pour plus de détail, cliquer sur les mots soulignés) :
-
Linéarisation des équations autour d'un état d'équilibre (indices 0), pour lequel on suppose une vitesse d'ensemble du plasma nulle, mais un champ magnétique, une densité, ... non nuls.
- Recherche d'une solution sous forme exponentielle : on suppose que toutes les petites perturbations obtenues par la linéarisation sont de la forme :
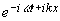
Ceci conduit à faire les remplacements suivants dans le système d'équations :
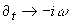
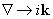
- Résolution du système homogène obtenu. La résolution est faite en éliminant toutes les variables au profit de la perturbation de vitesse. Ce système n'a une solution non triviale que si la pulsation et le vecteur d'onde vérifie une certaine relation, la relation de dispersion.
Pour simplifier l'écriture des résultats, on suppose que le repère de calcul est choisi de la manière suivante :
- Le champ magnétique est suivant l'axe z.
- Le vecteur d'onde est dans le plan (x,z) et il fait un angle avec le champ magnétique. On définit ainsi les deux composantes, parallèle et perpendiculaire, du vecteur d'onde.
La relation de dispersion obtenue s'écrit alors :
Cette équation possède trois paires de solutions, c'est à dire trois modes (l'équation est bicarrée à cause des deux sens de propagation de chaque mode). L'une des solutions est évidente, c'est celle qui correspond au terme central de la matrice. Pour cette solution, la pulsation et le vecteur d'onde doivent vérifier la relation :
On déduit aussi de la relation de dispersion que le vecteur de la perturbation de vitesse est suivant la direction y du repère. Des équations de départ on déduit les autres perturbations. elles sont dessinées sur la figure ci-dessous :