Détermination numérique des courbes de vitesse nulles
Introduction
Les courbes de vitesse nulle dans le cadre de notre étude du problème à trois corps restreint sont des courbes fermées du plan
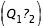
. Leur comportement topologique diffère suivant la valeur de J (voir chapitre précédent). Une fois ce comportement identifié, leur détermination numérique va donc se faire en trois étapes. On détermine tout d'abord un point de chacune des courbes que l'on considère, puis on suit le point trouvé le long de la courbe par continuation tout en définissant un paramètre de contrôle permettant l'arrêt de cette continuation (les courbes étant fermées).
Evaluation du comportement topologique des courbes de vitesse nulle suivant la valeur de J
Comme il est décrit au chapitre précèdent, il y a 5 comportement différents pour les courbes de vitesse nulle suivant la valeur de l'intégrale de Jacobi. Il convient donc de déterminer ces différents cas pour une détermination numérique appropriée des courbes.
Pour des conditions initiales données, et donc une intégrale de Jacobi J donnée, on rappelle que la courbe de vitesse nulle est définie par:
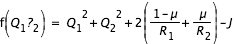
avec
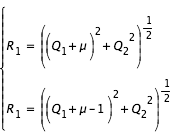
Les points de Lagrange
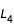
et
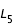
sont les premiers points où les courbes de vitesse nulle apparaissent. En se plaçant en
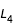
, on peut donc déterminer le seuil d'apparition des courbes.
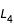
étant de coordonnées
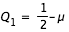
et
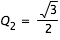
, on a
et
égaux à 1 et :
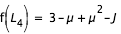
Les courbes de vitesse nulle existent donc pour:
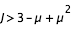
Les changement de topologies se font lorsque les différentes branches se touchent aux points de Lagrange. On peut donc déduire le nombre de branches à calculer en évaluant f en
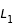
,
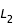
et
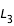
. On utilise bien sûr les valeurs numériques de
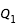
calculées lors de la détermination des points fixes,
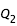
étant nul pour ces points. Ainsi :
- cas 1 : si
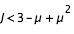 , il n'y a pas de courbes de vitesse nulle à déterminer.
, il n'y a pas de courbes de vitesse nulle à déterminer.
- cas 2 : si
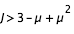 ,
, 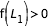 ,
, 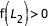 et
et 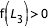 , on se trouve dans le cas où deux zones interdites symétrique se développent autour des points de Lagrange
, on se trouve dans le cas où deux zones interdites symétrique se développent autour des points de Lagrange 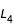 et
et 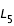 . Il suffit donc de déterminer celles autour de
. Il suffit donc de déterminer celles autour de 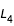 et la seconde est déduite directement par symétrie.
et la seconde est déduite directement par symétrie.
- cas 3 : si
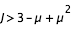 ,
, 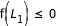 ,
, 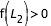 et
et 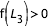 , ces deux zones se rejoignent autour de
, ces deux zones se rejoignent autour de 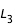 et la courbe de vitesse nulle forme une seule courbe en C fermée.
et la courbe de vitesse nulle forme une seule courbe en C fermée.
- cas 4 : si
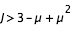 ,
, 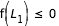 ,
, 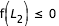 et
et 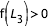 , la courbe en C se referme en
, la courbe en C se referme en 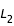 . Deux courbes de vitesse nulles sont à déterminer.
. Deux courbes de vitesse nulles sont à déterminer.
- cas 5 : enfin si
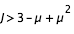 ,
, 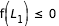 ,
, 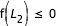 et
et 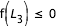 , la courbe finie par se refermée aussi en
, la courbe finie par se refermée aussi en 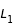 et alors trois courbes sont à déterminer, chacune contenant respectivement
et alors trois courbes sont à déterminer, chacune contenant respectivement 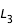 , la première et la seconde masse.
, la première et la seconde masse.
Recherche d'un point de départ pour la continuation d'une courbe
Afin de commencer la continuation de la courbe de vitesse nulle considérée, il nous faut d'abord trouver un point de cette courbe.
Pour cela on utilise les deux méthodes de détermination de zéro :
dichotomie et Newton-Raphson dans cet ordre pour les raisons exposées dans les chapitres leur correspondant. En effet en prenant un point à l'intérieur de la courbe (où f<0) et un autre à l'extérieur (où f>0), il existe un point dans cet intervalle tel que f=0 et qui appartient donc à la courbe de vitesse nulle.
Pour la méthode par dichotomie on choisit les intervalles de départ selon les cas topologiques comme suit:
- cas 2 : pour
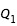 constant égale à
constant égale à 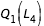 on effectue la recherche de zéro pour f entre
on effectue la recherche de zéro pour f entre 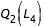 et
et 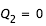
- cas 3 : idem
- cas 4 : pour la première courbe,
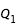 constant égale à
constant égale à 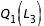 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 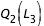 et
et 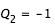 ; pour la seconde,
; pour la seconde, 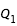 constant égale à
constant égale à 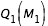 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 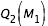 et
et 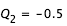
- cas 5 : pour la première courbe,
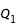 constant égale à
constant égale à 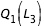 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 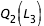 et
et 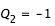 ; pour la seconde,
; pour la seconde, 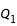 constant égale à
constant égale à 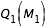 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 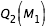 et
et 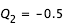 ; pour la troisième,
; pour la troisième, 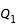 constant égale à
constant égale à 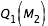 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 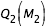 et
et 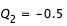
On démarre ensuite la méthode de Newton-Raphson depuis l'une des bornes de l'intervalle trouvé par dichotomie.
Continuation des courbes
Maintenant que l'on a trouvé un point de la courbe, on peut suivre le point trouvé le long de la courbe par "continuation". Pour cela écrivons un élément d'abscisse curviligne ds:
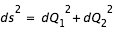
or
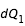
et
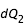
sont reliés via la différentielle de f :
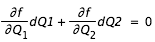
On déduit de ces deux équations le système suivant:
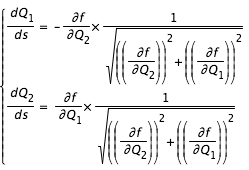
On a ainsi un système de deux équations différentielles à deux inconnues donnant l'évolution de
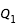
et
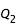
en fonction de s pouvant être résolu avec un intégrateur numérique(lien). On a choisi dans le calcul pour l'applet un Runge-Kutta d'ordre 4 à pas variable.
Remarque :
- Notez que le système a été écrit de façon à évitez une division par zéro,
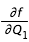 et
et 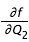 ne pouvant être nulles simultanément.
ne pouvant être nulles simultanément.
- On rappelle que :
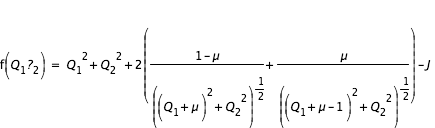
d'où
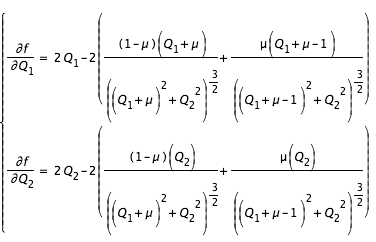
Arrêt de la continuation
Le problème auquel on est confronté lors de la continuation des courbes de vitesse nulle est lié au fait que ces courbes sont fermé et que l'intégrateur calculant les points de la courbe ne peut testé intrinsèquement si il est revenu à son point de départ ou non. Il nous faut donc trouver un moyen de tester ce paramètre afin d'éviter au programme de calculer pour rien, et/ou de passer à une étape suivante.
On effectue donc un changement d'origine du repère
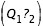
en le centrant sur un point à l'intérieur de la courbe, choisi astuscieusement en fonction des cas présentés plus haut. Pour différencier les axes de ce nouveau repère, on appellera x l'axe correspondant à
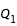
et y celui de
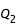
. Ainsi, lorsque l'ordonnée est négative (y<0) et l'abscisse change de signe (i.e. x<0 devient x>0), un angle de
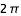
par rapport au premier point de la courbe est effectué. Autrement dit, la courbe se referme, on obtient une condition permettant de stopper la continuation.

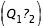 . Leur comportement topologique diffère suivant la valeur de J (voir chapitre précédent). Une fois ce comportement identifié, leur détermination numérique va donc se faire en trois étapes. On détermine tout d'abord un point de chacune des courbes que l'on considère, puis on suit le point trouvé le long de la courbe par continuation tout en définissant un paramètre de contrôle permettant l'arrêt de cette continuation (les courbes étant fermées).
. Leur comportement topologique diffère suivant la valeur de J (voir chapitre précédent). Une fois ce comportement identifié, leur détermination numérique va donc se faire en trois étapes. On détermine tout d'abord un point de chacune des courbes que l'on considère, puis on suit le point trouvé le long de la courbe par continuation tout en définissant un paramètre de contrôle permettant l'arrêt de cette continuation (les courbes étant fermées).
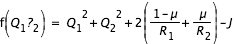
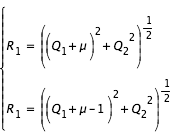
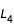 et
et 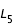 sont les premiers points où les courbes de vitesse nulle apparaissent. En se plaçant en
sont les premiers points où les courbes de vitesse nulle apparaissent. En se plaçant en 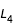 , on peut donc déterminer le seuil d'apparition des courbes.
, on peut donc déterminer le seuil d'apparition des courbes. 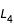 étant de coordonnées
étant de coordonnées 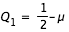 et
et 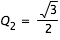 , on a
, on a 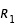 et
et 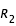 égaux à 1 et :
égaux à 1 et :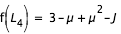
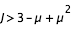
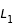 ,
, 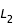 et
et 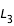 . On utilise bien sûr les valeurs numériques de
. On utilise bien sûr les valeurs numériques de 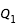 calculées lors de la détermination des points fixes,
calculées lors de la détermination des points fixes, 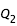 étant nul pour ces points. Ainsi :
étant nul pour ces points. Ainsi :
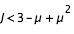 , il n'y a pas de courbes de vitesse nulle à déterminer.
, il n'y a pas de courbes de vitesse nulle à déterminer.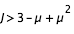 ,
, 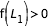 ,
, 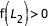 et
et 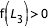 , on se trouve dans le cas où deux zones interdites symétrique se développent autour des points de Lagrange
, on se trouve dans le cas où deux zones interdites symétrique se développent autour des points de Lagrange 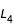 et
et 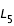 . Il suffit donc de déterminer celles autour de
. Il suffit donc de déterminer celles autour de 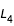 et la seconde est déduite directement par symétrie.
et la seconde est déduite directement par symétrie.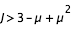 ,
, 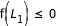 ,
, 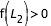 et
et 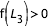 , ces deux zones se rejoignent autour de
, ces deux zones se rejoignent autour de 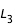 et la courbe de vitesse nulle forme une seule courbe en C fermée.
et la courbe de vitesse nulle forme une seule courbe en C fermée.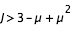 ,
, 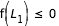 ,
, 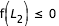 et
et 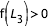 , la courbe en C se referme en
, la courbe en C se referme en 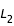 . Deux courbes de vitesse nulles sont à déterminer.
. Deux courbes de vitesse nulles sont à déterminer.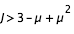 ,
, 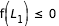 ,
, 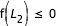 et
et 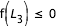 , la courbe finie par se refermée aussi en
, la courbe finie par se refermée aussi en 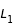 et alors trois courbes sont à déterminer, chacune contenant respectivement
et alors trois courbes sont à déterminer, chacune contenant respectivement 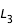 , la première et la seconde masse.
, la première et la seconde masse.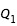 constant égale à
constant égale à 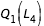 on effectue la recherche de zéro pour f entre
on effectue la recherche de zéro pour f entre 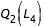 et
et 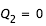
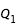 constant égale à
constant égale à 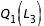 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 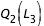 et
et 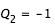 ; pour la seconde,
; pour la seconde, 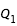 constant égale à
constant égale à 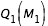 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 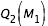 et
et 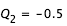
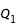 constant égale à
constant égale à 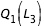 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 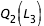 et
et 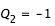 ; pour la seconde,
; pour la seconde, 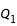 constant égale à
constant égale à 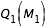 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 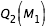 et
et 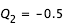 ; pour la troisième,
; pour la troisième, 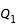 constant égale à
constant égale à 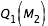 , on effectue la recherche de zéro pour f entre
, on effectue la recherche de zéro pour f entre 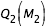 et
et 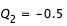
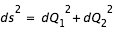
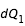 et
et 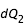 sont reliés via la différentielle de f :
sont reliés via la différentielle de f :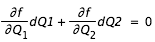
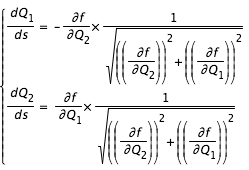
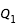 et
et 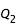 en fonction de s pouvant être résolu avec un intégrateur numérique(lien). On a choisi dans le calcul pour l'applet un Runge-Kutta d'ordre 4 à pas variable.
en fonction de s pouvant être résolu avec un intégrateur numérique(lien). On a choisi dans le calcul pour l'applet un Runge-Kutta d'ordre 4 à pas variable.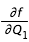 et
et 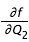 ne pouvant être nulles simultanément.
ne pouvant être nulles simultanément.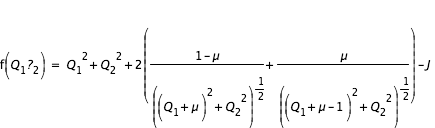
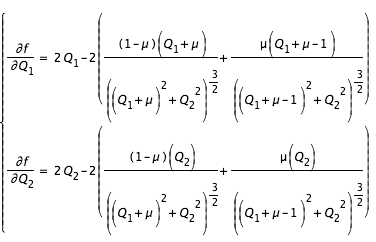
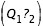 en le centrant sur un point à l'intérieur de la courbe, choisi astuscieusement en fonction des cas présentés plus haut. Pour différencier les axes de ce nouveau repère, on appellera x l'axe correspondant à
en le centrant sur un point à l'intérieur de la courbe, choisi astuscieusement en fonction des cas présentés plus haut. Pour différencier les axes de ce nouveau repère, on appellera x l'axe correspondant à 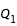 et y celui de
et y celui de 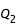 . Ainsi, lorsque l'ordonnée est négative (y<0) et l'abscisse change de signe (i.e. x<0 devient x>0), un angle de
. Ainsi, lorsque l'ordonnée est négative (y<0) et l'abscisse change de signe (i.e. x<0 devient x>0), un angle de 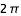 par rapport au premier point de la courbe est effectué. Autrement dit, la courbe se referme, on obtient une condition permettant de stopper la continuation.
par rapport au premier point de la courbe est effectué. Autrement dit, la courbe se referme, on obtient une condition permettant de stopper la continuation.