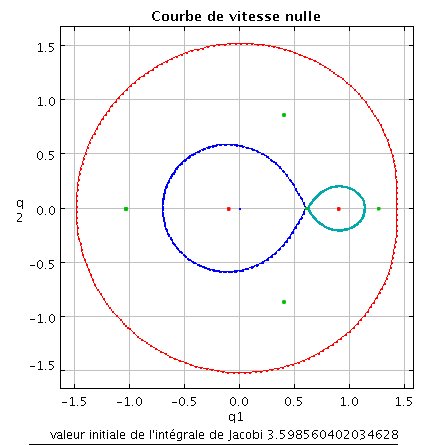
Caracterisation et détermination des courbes de vitesse nulle
L'expression de l'Hamiltonien peut se réécrire sous une forme différente, en réintroduisant les vitesses relatives dans le référentiel en rotation
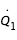
et
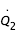
, on obtient alors :
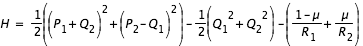
Puisque
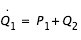
et
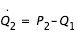
, et que la courbe de vitesse nulle s'écrit
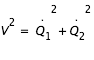
,
nous obtenons :
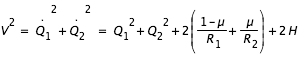
Or, nous avons l'intégrale de Jacobi (lien) qui vaut J=-2H.
L'équation de la courbe de vitesse nulle est donc la suivante :
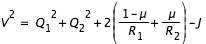
Cette expression devant être toujours positive, on voit que pour une valeur fixée de J, le plan (Q
1,Q
2) sera partagé en plusieurs régions:
- Celles où l'équation précédente est négative sont des zones où le mouvement n'est pas possible, ce sont des zones interdites.
- Les points (Q1,Q2) pour lesquels l'expression précédente s'annule forment les séparatrices appelées "courbes de vitesse nulle". Notons que ces séparatrices ne sont pas interdites ! En effet, le fait que la vitesse s'y annule ne signifie pas que l'accélération soit elle aussi nulle. Les trajectoires de la particule peuvent donc passées par un point de ces courbes, où elles sont tangentes.
Bien entendu, ces courbes ne sont visible que dans le repère tournant.

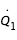 et
et 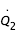 , on obtient alors :
, on obtient alors : 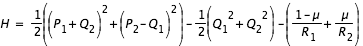
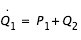 et
et 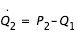 , et que la courbe de vitesse nulle s'écrit
, et que la courbe de vitesse nulle s'écrit 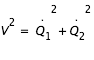 ,
,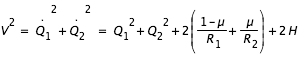
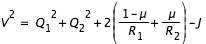
 et
et  .
. .
.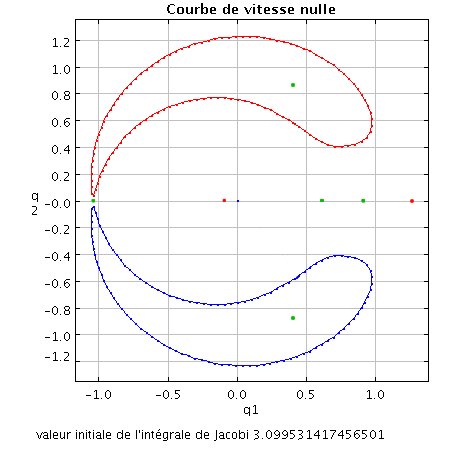
 . Le plan (Q1,Q2) est alors séparé en deux régions qui ne peuvent communiquer entre elles. Si la sonde est lâchée au voisinage d'un des deux corps massif, elle ne peut s'échapper.
. Le plan (Q1,Q2) est alors séparé en deux régions qui ne peuvent communiquer entre elles. Si la sonde est lâchée au voisinage d'un des deux corps massif, elle ne peut s'échapper.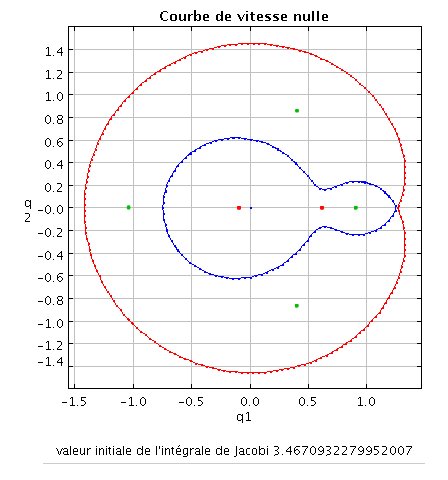
 de celui de
de celui de 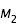 . La sonde est alors confinée au voisinage d'une seule des deux masses.
. La sonde est alors confinée au voisinage d'une seule des deux masses.