Intégrale de Jacobi
L'intégrale de Jacobi
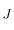
est définie par
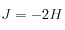
, où
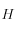
est le
Hamiltonien du système. C'est donc une intégrale première du mouvement. Cela se traduit dans l'espace des phases
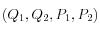
par le fait que le système doive rester sur la variété (de dimension 3)
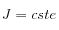
au cours du temps. Cette contrainte sur l'évolution est particulièrement importante lorsque l'on s'intéresse à l'évolution du système sur le long terme, par exemple lorsque l'on étudie des sections de Poincaré.
L'
intégrateur Runge-Kutta d'ordre 4 à pas variable utilisé ici ne conserve pas cette quantité. Sur l'applet, on observe effectivement une dérive constante de cette valeur. L'autre intégrateur disponible est de type Runge-Kutta d'ordre 4, à pas fixe,
symplectique, qui lui conserve l'intégrale de Jacobi. On observe effectivement une plus grande stabilité de cette dernière sur les simulations de l'applet. Si l'on cherche à tracer des sections de Poincaré du système, il faudra donc utiliser l'intégrateur symplectique.

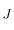 est définie par
est définie par 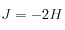 , où
, où 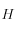 est le Hamiltonien du système. C'est donc une intégrale première du mouvement. Cela se traduit dans l'espace des phases
est le Hamiltonien du système. C'est donc une intégrale première du mouvement. Cela se traduit dans l'espace des phases 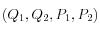 par le fait que le système doive rester sur la variété (de dimension 3)
par le fait que le système doive rester sur la variété (de dimension 3) 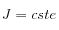 au cours du temps. Cette contrainte sur l'évolution est particulièrement importante lorsque l'on s'intéresse à l'évolution du système sur le long terme, par exemple lorsque l'on étudie des sections de Poincaré.
L'intégrateur Runge-Kutta d'ordre 4 à pas variable utilisé ici ne conserve pas cette quantité. Sur l'applet, on observe effectivement une dérive constante de cette valeur. L'autre intégrateur disponible est de type Runge-Kutta d'ordre 4, à pas fixe, symplectique, qui lui conserve l'intégrale de Jacobi. On observe effectivement une plus grande stabilité de cette dernière sur les simulations de l'applet. Si l'on cherche à tracer des sections de Poincaré du système, il faudra donc utiliser l'intégrateur symplectique.
au cours du temps. Cette contrainte sur l'évolution est particulièrement importante lorsque l'on s'intéresse à l'évolution du système sur le long terme, par exemple lorsque l'on étudie des sections de Poincaré.
L'intégrateur Runge-Kutta d'ordre 4 à pas variable utilisé ici ne conserve pas cette quantité. Sur l'applet, on observe effectivement une dérive constante de cette valeur. L'autre intégrateur disponible est de type Runge-Kutta d'ordre 4, à pas fixe, symplectique, qui lui conserve l'intégrale de Jacobi. On observe effectivement une plus grande stabilité de cette dernière sur les simulations de l'applet. Si l'on cherche à tracer des sections de Poincaré du système, il faudra donc utiliser l'intégrateur symplectique.