Intégrateur RK4 symplectique à pas fixe
Définition d'un intégrateur symplectique
On cherche à résoudre numériquement l'équation :
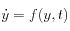
.
Un intégrateur numérique est dit symplectique s'il conserve la structure hamiltonienne des
équations, c'est-à-dire les expressions des
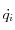
et des
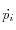
.
Il conserve en particulier le Hamiltonien
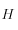
(qui représente l'énergie du système) et donc l'intégrale de Jacobi.
Un choix de conditions initiales du système place la particule étudiée sur une variété d'énergie précise dans l'espace des phases. L'intégrateur symplectique nous assure alors de rester sur celle-ci.
Définition du RK4 symplectique à pas fixe
Un tel intégrateur se construit en choisissant judicieusement les points où l'on évalue la fonction
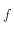
entre deux itérations. Ces derniers sont au nombre de trois (différents du point de départ
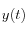
), et sont notés
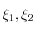
et
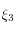
.
On passe alors du point
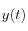
au point
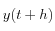
via la relation :
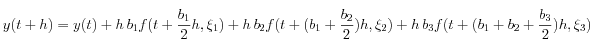
où les
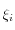
sont donnés par les expressions suivantes :
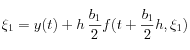
,
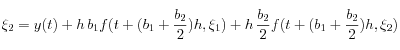
,
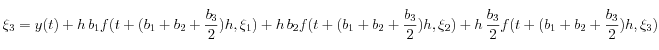
et où les
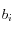
valent (pour la méthode choisie; réf : "Numerical Hamiltonian Problems", J.M. Sanz-Serna et M.P. Calvo, p. 102) :
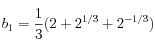
,
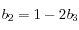
,
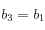
Les
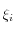
sont donnés implicitement; on parle alors de
méthode implicite. Précisons qu'un intégrateur symplectique est forcément implicite (ibid.).
La méthode est dite "DIRK" (Diagonally Implicit Runge-Kutta methods) : la relation définissant
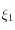
ne fait apparaître ni
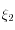
ni
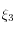
, et celle définissant
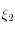
ne fait pas intervenir
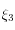
. On peut donc d'abord déterminer
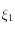
, puis
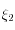
, et enfin
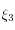
.
Implémentation
Les coefficients
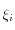
ont été calculé par l'algorithme de Newton "classique".
Pour le système étudié ici, la fonction
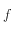
(l'équation du mouvement) est autonome, c'est-à-dire qu'elle ne dépend pas du temps.
L'algorithme de Newton a donc d'abord été appliqué à la fonction
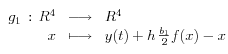
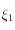
est alors la solution (sous réserve d'existence et d'unicité) de
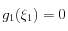
.
On détermine ensuite
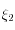
comme zéro de la fonction
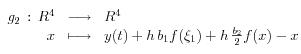
puis
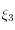
comme zéro de
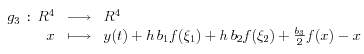
On peut alors calculer
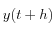
.
En réitérant ce processus, on peut alors déterminer la trajectoire complète de la particule.

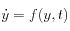 .
Un intégrateur numérique est dit symplectique s'il conserve la structure hamiltonienne des équations, c'est-à-dire les expressions des
.
Un intégrateur numérique est dit symplectique s'il conserve la structure hamiltonienne des équations, c'est-à-dire les expressions des 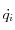 et des
et des 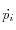 .
Il conserve en particulier le Hamiltonien
.
Il conserve en particulier le Hamiltonien 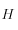 (qui représente l'énergie du système) et donc l'intégrale de Jacobi.
Un choix de conditions initiales du système place la particule étudiée sur une variété d'énergie précise dans l'espace des phases. L'intégrateur symplectique nous assure alors de rester sur celle-ci.
(qui représente l'énergie du système) et donc l'intégrale de Jacobi.
Un choix de conditions initiales du système place la particule étudiée sur une variété d'énergie précise dans l'espace des phases. L'intégrateur symplectique nous assure alors de rester sur celle-ci.
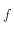 entre deux itérations. Ces derniers sont au nombre de trois (différents du point de départ
entre deux itérations. Ces derniers sont au nombre de trois (différents du point de départ 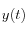 ), et sont notés
), et sont notés 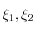 et
et 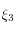 .
.
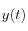 au point
au point 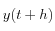 via la relation :
via la relation :
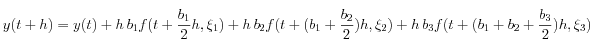
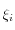 sont donnés par les expressions suivantes :
sont donnés par les expressions suivantes :
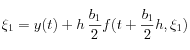 ,
,
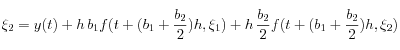 ,
,
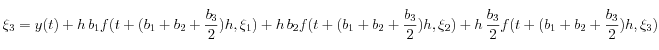
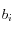 valent (pour la méthode choisie; réf : "Numerical Hamiltonian Problems", J.M. Sanz-Serna et M.P. Calvo, p. 102) :
valent (pour la méthode choisie; réf : "Numerical Hamiltonian Problems", J.M. Sanz-Serna et M.P. Calvo, p. 102) :
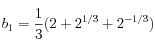 ,
,
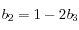 ,
,
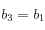
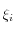 sont donnés implicitement; on parle alors de méthode implicite. Précisons qu'un intégrateur symplectique est forcément implicite (ibid.).
La méthode est dite "DIRK" (Diagonally Implicit Runge-Kutta methods) : la relation définissant
sont donnés implicitement; on parle alors de méthode implicite. Précisons qu'un intégrateur symplectique est forcément implicite (ibid.).
La méthode est dite "DIRK" (Diagonally Implicit Runge-Kutta methods) : la relation définissant 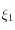 ne fait apparaître ni
ne fait apparaître ni 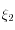 ni
ni 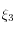 , et celle définissant
, et celle définissant 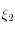 ne fait pas intervenir
ne fait pas intervenir 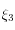 . On peut donc d'abord déterminer
. On peut donc d'abord déterminer 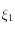 , puis
, puis 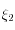 , et enfin
, et enfin 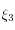 .
.
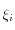 ont été calculé par l'algorithme de Newton "classique".
Pour le système étudié ici, la fonction
ont été calculé par l'algorithme de Newton "classique".
Pour le système étudié ici, la fonction 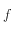 (l'équation du mouvement) est autonome, c'est-à-dire qu'elle ne dépend pas du temps.
L'algorithme de Newton a donc d'abord été appliqué à la fonction
(l'équation du mouvement) est autonome, c'est-à-dire qu'elle ne dépend pas du temps.
L'algorithme de Newton a donc d'abord été appliqué à la fonction
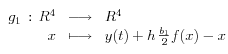
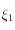 est alors la solution (sous réserve d'existence et d'unicité) de
est alors la solution (sous réserve d'existence et d'unicité) de 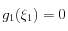 .
.
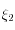 comme zéro de la fonction
comme zéro de la fonction
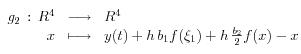
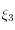 comme zéro de
comme zéro de
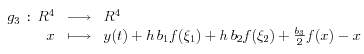
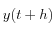 .
En réitérant ce processus, on peut alors déterminer la trajectoire complète de la particule.
.
En réitérant ce processus, on peut alors déterminer la trajectoire complète de la particule.