Sections de Poincaré
La section de Poincaré est souvent utilisé pour caractériser le chaos, et étudier la dynamique d'un système. Pour définir cette section de Poincaré dans le cadre du problème à trois corps restreint, rappelons nous qu'on s'intéresse à la particule test, dans le repère tournant. Il est alors intéressant de reporter sur un diagramme les valeurs (q1,p1) de cette particule à chaque fois qu'elle coupe l'axe q2=0. On dit alors que la section de Poincaré est à q2=0.
Plus généralement, une section de Poincaré se dessine dans un plan ayant pour abscisse la coordonnée généralisé
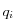
et pour ordonnée la coordonnée généralisé
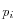
(ou, quand le problème permet une formulation hamiltonienne en coordonnées action-angle : (angle-action)),
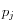
(j
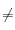
i) étant calculés pour que J=cste (on parle alors de variété d'énergie sur laquelle on se place, ie. une section de Poincaré est un ensemble de trajectoires à énergie constante), et
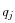
(j
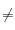
i) étant libre. La section est alors généralement une surface de section (ie. équation de plusieurs variables).
Dans notre cas, il est intéressant de tracer une section de Poincaré à q2=0.
Par ailleurs, on définit une trajectoire de Poincaré, les points de ce diagramme issus de même conditions initiales q10, q20, p10, p20. On fixe généralement q20 une fois pour toute, et on calcule p20 en fonction de q10, p10 et J (qui doit rester constant sur toutes les trajectoires). Plus le nombre de points d'une trajectoire de Poincaré est élevé, plus la section de Poincaré est claire à l'interprétation.
On obtient alors des courbes fermées (si le nombre de trajectoires de Poincaré est suffisant) correspondant à l'ensemble des valeurs des couples (q1,p1) prises par la particule test quand elle suit une orbite non-chaotique, et des zones chaotiques caractérisées par une densité de points non ordonnés élevée, et prises entre deux courbes fermées.
Les zones chaotiques entourent généralement un ensemble de courbes fermées, appelé île. De même, les zones où l'on retrouve des courbes fermées à l'intérieur d'une zone chaotique entourant une île sont des zones de résonances (librations).

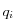 et pour ordonnée la coordonnée généralisé
et pour ordonnée la coordonnée généralisé 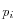 (ou, quand le problème permet une formulation hamiltonienne en coordonnées action-angle : (angle-action)),
(ou, quand le problème permet une formulation hamiltonienne en coordonnées action-angle : (angle-action)), 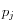 (j
(j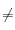 i) étant calculés pour que J=cste (on parle alors de variété d'énergie sur laquelle on se place, ie. une section de Poincaré est un ensemble de trajectoires à énergie constante), et
i) étant calculés pour que J=cste (on parle alors de variété d'énergie sur laquelle on se place, ie. une section de Poincaré est un ensemble de trajectoires à énergie constante), et 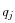 (j
(j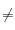 i) étant libre. La section est alors généralement une surface de section (ie. équation de plusieurs variables).
i) étant libre. La section est alors généralement une surface de section (ie. équation de plusieurs variables).