Obtention d'une formulation hamiltonienne adimensionnée et autonome
Nous résumons ici les étapes nécessaires à l'obtention de la formulation hamiltonienne que nous utilisons par la suite. Le détail des calculs est donné
ici.
On écrit tout d'abord le Lagrangien associé au mouvement de la particule dans le champ gravitationnel créé par les deux masses
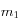
et
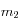
.
Afin de simplifier les expressions obtenues, on procède à un "dédimensionnement" des équations ; les constantes du problème sont alors incluses dans les variables et celles-ci deviennent dimensionnées.
Bien que la formulation lagrangienne permette de décrire le système, la formulation hamiltonienne, plus adaptée aux problèmes de mécanique céleste, va être privilégiée ici. On dérive ainsi du Lagrangien le Hamiltonien associé au problème.
Cependant, celui-ci dépend du temps. On le rend autonome (sans dépendance explicite du temps) via une transformation canonique (changement de variables qui préserve la structure hamiltonienne).

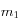 et
et 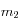 .
Afin de simplifier les expressions obtenues, on procède à un "dédimensionnement" des équations ; les constantes du problème sont alors incluses dans les variables et celles-ci deviennent dimensionnées.
Bien que la formulation lagrangienne permette de décrire le système, la formulation hamiltonienne, plus adaptée aux problèmes de mécanique céleste, va être privilégiée ici. On dérive ainsi du Lagrangien le Hamiltonien associé au problème.
Cependant, celui-ci dépend du temps. On le rend autonome (sans dépendance explicite du temps) via une transformation canonique (changement de variables qui préserve la structure hamiltonienne).
.
Afin de simplifier les expressions obtenues, on procède à un "dédimensionnement" des équations ; les constantes du problème sont alors incluses dans les variables et celles-ci deviennent dimensionnées.
Bien que la formulation lagrangienne permette de décrire le système, la formulation hamiltonienne, plus adaptée aux problèmes de mécanique céleste, va être privilégiée ici. On dérive ainsi du Lagrangien le Hamiltonien associé au problème.
Cependant, celui-ci dépend du temps. On le rend autonome (sans dépendance explicite du temps) via une transformation canonique (changement de variables qui préserve la structure hamiltonienne).