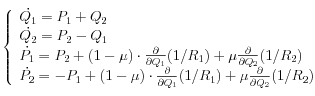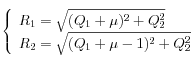Formulation hamiltonienne du problème
Le Hamiltonien
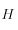
finalement obtenu s'écrit :
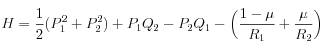
avec comme équations associées :

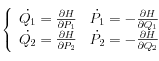
Les variables
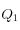
et
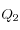
se rapportent à la position de la particule,
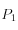
et
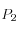
sont leurs variables dites "conjuguées" et sont liées à la vitesse de la particule.
Le Hamiltonien
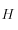
représente en fait l'énergie du système. Théoriquement, il doit donc être conservé au cours du mouvement. On dit alors qu'il constitue une intégrale première du mouvement.
Explicitement, les équations du mouvement sont donc :
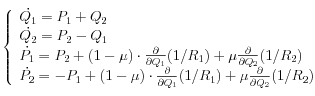
où
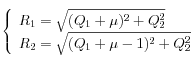

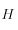 finalement obtenu s'écrit :
finalement obtenu s'écrit :
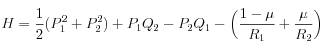

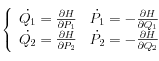
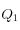 et
et 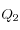 se rapportent à la position de la particule,
se rapportent à la position de la particule, 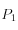 et
et 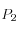 sont leurs variables dites "conjuguées" et sont liées à la vitesse de la particule.
Le Hamiltonien
sont leurs variables dites "conjuguées" et sont liées à la vitesse de la particule.
Le Hamiltonien 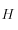 représente en fait l'énergie du système. Théoriquement, il doit donc être conservé au cours du mouvement. On dit alors qu'il constitue une intégrale première du mouvement.
Explicitement, les équations du mouvement sont donc :
représente en fait l'énergie du système. Théoriquement, il doit donc être conservé au cours du mouvement. On dit alors qu'il constitue une intégrale première du mouvement.
Explicitement, les équations du mouvement sont donc :