Observables
A partir de ahora:
- Nos limitamos al caso de las órbitas circulares de radio
 .
.
- Denotamos
 a la masa del planeta, y
a la masa del planeta, y
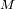 a la de la estrella.
a la de la estrella.
Se supone que, según los modelos estelares, la medida del
espectro de la estrella
permite estimar su masa
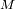
. Pero no se conoce una variable:
la inclinación

bajo la cual se ve el sistema orbital.
Las principales características de la órbita del planeta pueden ser deducidas a partir de la medida del
desplazamiento Doppler.
El análisis del espectro de la estrella modulado por
efecto Doppler
permite obtener la
gráfica de la velocidad radial
de la estrella en función del tiempo,
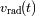
.
Este tipo de observación espectrométrica nos proporciona dos
observables:
- La componente de velocidad de la estrella
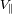 , paralela al eje de observación (puesto que el efecto Doppler
es sensible a la única componente
, paralela al eje de observación (puesto que el efecto Doppler
es sensible a la única componente
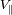 ).
).
- El periodo
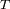 de rotación del sistema.
de rotación del sistema.
Estos observables son características ligadas a la órbita del sistema. Todavía no se sabe nada sobre el
planeta en sí. La tercera ley de Kepler aplicada a la pareja planeta-estrella relaciona el radio de la
órbita con el periodo de rotación:
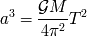
Utilizando la ley de conservación de la cantidad de movimiento (
el sistema está aislado), se puede
averiguar la masa del planeta:
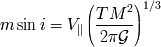
donde
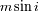
es la masa del planeta
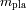
afectada del factor geométrico
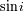
, desconocido. El cálculo completo está hecho en un
ejercicio.
Inclinación
Estadísticamente, la probabilidad de tener una inclinación

depende de la apertura del cono de semiángulo

: esta probabilidad vale
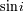
. Es más probable ver un sistema
de cara
que
de lado
(i=0).
De media, el parámetro
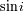
vale
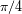
; este cálculo está propuesto en un
ejercicio.

 .
.
 a la masa del planeta, y
a la masa del planeta, y
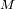 a la de la estrella.
a la de la estrella.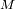 . Pero no se conoce una variable: la inclinación
. Pero no se conoce una variable: la inclinación
 bajo la cual se ve el sistema orbital.
Las principales características de la órbita del planeta pueden ser deducidas a partir de la medida del
desplazamiento Doppler.
bajo la cual se ve el sistema orbital.
Las principales características de la órbita del planeta pueden ser deducidas a partir de la medida del
desplazamiento Doppler.
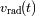 .
Este tipo de observación espectrométrica nos proporciona dos observables:
.
Este tipo de observación espectrométrica nos proporciona dos observables:
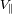 , paralela al eje de observación (puesto que el efecto Doppler
es sensible a la única componente
, paralela al eje de observación (puesto que el efecto Doppler
es sensible a la única componente
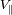 ).
).
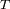 de rotación del sistema.
de rotación del sistema.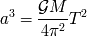
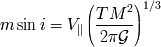
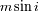 es la masa del planeta
es la masa del planeta
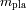 afectada del factor geométrico
afectada del factor geométrico
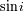 , desconocido. El cálculo completo está hecho en un ejercicio.
, desconocido. El cálculo completo está hecho en un ejercicio.