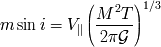Ejercicio 'La velocimetría Doppler'
Ejercicio 'La velocimetría Doppler'
Nivel **
Tiempo necesario :
45 min
Esta técnica permite la detección de planetas a partir de
la perturbación en velocidad
(velocidad reflejo) que introducen en su estrella.
Se observa un sistema constituido por un planeta de masa

en órbita circular alrededor de una estrella de masa
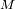
. La componente de velocidad de la estrella
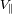
, paralela al eje de observación, así como el periodo de rotación del sistema se derivan a partir de la
observación. Se supone que la masa
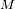
es conocida.
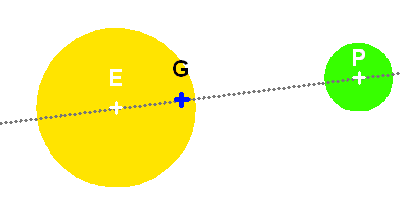
Esquema del sistema
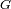 ,
,
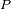 y
y
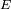 son la posición del baricentro del sistema, del centro de masas del planeta y del
centro de masas de la estrella, respectivamente.
son la posición del baricentro del sistema, del centro de masas del planeta y del
centro de masas de la estrella, respectivamente.
Crédito : Astrophysique sur Mesure
1)
Definir la posición del baricentro del sistema estrella-planeta.
Demostrar que, en el referencial baricéntrico, las velocidades
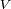
de la estrella y

del planeta satisfacen la relación:
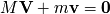 ayuda
ayuda
solución
ayuda
ayuda
solución
2)
Dar la relación que relaciona
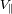
con el módulo
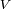
de la velocidad de la estrella y el ángulo

entre el eje de observación y la normal al plano de rotación del sistema. Hacer un
esquema.
ayuda
solución
5)
Sustituir en el observable
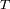
la variable

, y demostrar que se llega a la identidad siguiente entre las variables

y
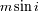
:
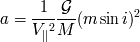 ayuda
solución
ayuda
solución

 es proporcional a
es proporcional a
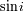 .
solución
.
solución
 en órbita circular alrededor de una estrella de masa
en órbita circular alrededor de una estrella de masa
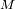 . La componente de velocidad de la estrella
. La componente de velocidad de la estrella
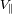 , paralela al eje de observación, así como el periodo de rotación del sistema se derivan a partir de la
observación. Se supone que la masa
, paralela al eje de observación, así como el periodo de rotación del sistema se derivan a partir de la
observación. Se supone que la masa
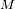 es conocida.
es conocida.

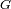 ,
,
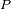 y
y
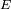 son la posición del baricentro del sistema, del centro de masas del planeta y del
centro de masas de la estrella, respectivamente.
son la posición del baricentro del sistema, del centro de masas del planeta y del
centro de masas de la estrella, respectivamente.
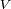 de la estrella y
de la estrella y
 del planeta satisfacen la relación:
del planeta satisfacen la relación:
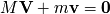
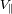 con el módulo
con el módulo
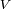 de la velocidad de la estrella y el ángulo
de la velocidad de la estrella y el ángulo
 entre el eje de observación y la normal al plano de rotación del sistema. Hacer un
esquema.
ayuda
solución
entre el eje de observación y la normal al plano de rotación del sistema. Hacer un
esquema.
ayuda
solución
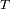 y
y
 . A continuación demostrar que la masa del planeta se expresa en función de los observables
. A continuación demostrar que la masa del planeta se expresa en función de los observables
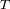 y
y
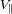 según:
según: