 Objetivos
Objetivos
En los años 80, los primeros trabajo utilizando la relación de Tully-Fisher obtiene un valor alto de la constante
de Hubble - del orden de 100 km/s/Mpc - así que un crecimiento de
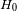
con la distancia. Estos resultados provienen de la naturaleza estadística de la relación de Tully-Fisher y del
hecho de que las muestras son siempre limitadas en magnitud aparente.
Propriedad estadística
Todos las galaxias poseyendo la misma velocidad de rotación
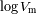
(o perteneciendo a una clase de similares), les atribuimos la misma magnitud absoluta (o
luminosidad) según la relación lineal :
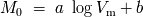
Cada determinación individual sufre de hecho una imprecisión debida a la diferencia entre
la magnitud absoluta exacta y el valor medio
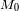
adoptado. Ahora, si consideramos un gran número de objetos, unos siendo sobreestimados,
los otros siendos subestimados. Si embargo, se espera que sean exactas
en media.
Sesgo de Malmquist
K.G. Malmquist (1920) desmostró que no es el caso si la muestra utilizada está limitada en
magnitud aparente : la muestra contiene en efecto una más grande proporción de galaxias
intrísecamente más luminosas que
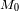
, y una menor proporción de galaxias menos luminosas. La magnitud absoluta media del
conjunto de galaxias del catálogo no es igual, sino inferior a
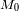
.
Se sigue que subestimando así la luminosidad media de las galaxias observadas, se subestiman
sus distancias, y se sobreestima la constante de Hubble.
Error estadístico
Si se supone que las galaxias están repartidas uniformemente en el espacio, el error estadístico
de la magnitud absoluta
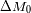
y entonces de su módulo de distancia de las galaxias puede expresarse de manera sencilla en
función de la dispersión

del criterio de distancia (la incertidumbre media con respecto a
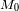
) :
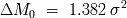
Para una dispersión

de orden 0.6 de magnitud, típicamente lo que se obtiene por la
relación de Tully-Fisher
o el
método de las similares,
es un error sobre el módulo de distancia de -0.5 de magnitud. Se obtiene finalmente una subestimación
de la distancia del orden de 23% , y un valor de
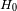
sobreestimado.

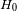 con la distancia. Estos resultados provienen de la naturaleza estadística de la relación de Tully-Fisher y del
hecho de que las muestras son siempre limitadas en magnitud aparente.
con la distancia. Estos resultados provienen de la naturaleza estadística de la relación de Tully-Fisher y del
hecho de que las muestras son siempre limitadas en magnitud aparente. 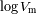 (o perteneciendo a una clase de similares), les atribuimos la misma magnitud absoluta (o
luminosidad) según la relación lineal :
(o perteneciendo a una clase de similares), les atribuimos la misma magnitud absoluta (o
luminosidad) según la relación lineal :
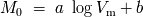
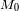 adoptado. Ahora, si consideramos un gran número de objetos, unos siendo sobreestimados,
los otros siendos subestimados. Si embargo, se espera que sean exactas en media.
adoptado. Ahora, si consideramos un gran número de objetos, unos siendo sobreestimados,
los otros siendos subestimados. Si embargo, se espera que sean exactas en media.
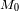 , y una menor proporción de galaxias menos luminosas. La magnitud absoluta media del
conjunto de galaxias del catálogo no es igual, sino inferior a
, y una menor proporción de galaxias menos luminosas. La magnitud absoluta media del
conjunto de galaxias del catálogo no es igual, sino inferior a
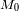 .
.
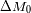 y entonces de su módulo de distancia de las galaxias puede expresarse de manera sencilla en
función de la dispersión
y entonces de su módulo de distancia de las galaxias puede expresarse de manera sencilla en
función de la dispersión
 del criterio de distancia (la incertidumbre media con respecto a
del criterio de distancia (la incertidumbre media con respecto a
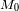 ) :
) :
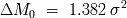
 de orden 0.6 de magnitud, típicamente lo que se obtiene por la relación de Tully-Fisher
o el método de las similares,
es un error sobre el módulo de distancia de -0.5 de magnitud. Se obtiene finalmente una subestimación
de la distancia del orden de 23% , y un valor de
de orden 0.6 de magnitud, típicamente lo que se obtiene por la relación de Tully-Fisher
o el método de las similares,
es un error sobre el módulo de distancia de -0.5 de magnitud. Se obtiene finalmente una subestimación
de la distancia del orden de 23% , y un valor de
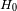 sobreestimado.
sobreestimado.