Apprendre

Objectifs

Définir le rayonnement du corps noir
Le corps est finalement une entité physique idéale, dont le rayonnement ne se caractérise plus que par sa température d'équilibre
Les définitions des grandeurs énergétiques utiles sont rappelées à la page de photométrie énergétique.

La loi de Planck

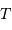
La loi de Planck décrit l'émission d'un corps noir de température :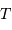

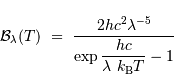
${{ \mathcal{B}}}_\lambda (T) \ =\ {2 h c^{2} \lambda^{-5} \over \exp\displaystyle{hc\over \lambda\ k _{\mathrm{B}}T} -1}$

Interviennent dans cette relation la constante de Planck 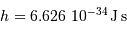$h = 6.626\ 10^{-34} {\,\mathrm{J}} {\,\mathrm{s}}$ , la constante de Boltzmann 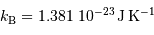$k _{\mathrm{B}} = 1.381\ 10^{-23} {\,\mathrm{J}} { {\,\mathrm{K}}}^{-1}$ , et 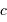la célérité de la lumière dans le vide. Ceci indique que la loi de Planck est à l'intersection, respectivement, de la physique quantique, statistique et relativiste.

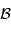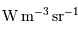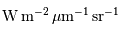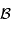Dans le système d'unités international, ${{ \mathcal{B}}}$ s'exprime en ${\,\mathrm{W}}{ {\,\mathrm{m}}}^{-3}{ {\,\mathrm{sr}}}^{-1}$ , ou en unité dérivée ${\,\mathrm{W}} {\,\mathrm{m}}^{-2} {\,\mu\mathrm{m}}^{-1} {\,\mathrm{sr}}^{-1}$ ; $\mathcal{B}$ est une luminance spectrale, càd une puissance rayonnée par unités d'angle solide, de surface et spectrale.

Le dénominateur de la loi de Planck est caractéristique d'une loi statistique de Bose-Einstein, à laquelle obéit un gaz de photons. Comme tout vecteur d'interaction fondamentale (l'interaction électromagnétique), le photon est un boson, une particule de spin entier.

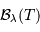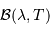La fonction ${ \mathcal{B}}_\lambda (T)$ dépend de la température comme de la longueur d'onde. Elle est notée ainsi, et non ${ \mathcal{B}} (\lambda, T)$ , pour mettre en évidence la variable spectrale, ici la longueur d'onde. Cette dépendance spectrale peut également s'exprimer en fonction non de la longueur d'onde, mais de la fréquence. La loi de Planck se réécrit alors dans ce cas (justification donnée en exercice).

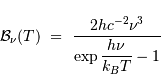
${{ \mathcal{B}}}_\nu (T) \ =\ {2 h c^{-2} \nu^{3}\over \exp\displaystyle{h\nu\over k_BT} -1}$

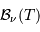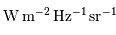L'unité de ${{ \mathcal{B}}}_\nu (T)$ est alors : ${\,\mathrm{W}} {\,\mathrm{m}}^{-2} {\,\mathrm{Hz}}^{-1} {\,\mathrm{sr}}^{-1}$ .