Conclusion

On voit donc que la hauteur h est une fonction des deux paramètres φ (latitude du lieu) et δ (déclinaison de l'astre) et qu’elle doit être toujours comprise entre –90° et 90°. On est donc toujours ramené à résoudre les quatre équations et à conserver les solutions qui donnent une hauteur comprise entre –90° et 90°. Le tableau suivant résume ces quatre possibilités.

Solutions pour les passages au méridien

Passage au méridien supérieur	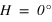		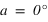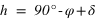équation (1)
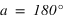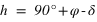			équation (2)
Passage au méridien inférieur	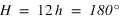		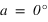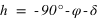équation (3)
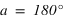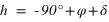			équation (4)

À l’aide de ces formules, on peut, soit se placer en un lieu donné (en fixant φ) et étudier les passages au méridien des corps en fonction de leurs déclinaisons, soit choisir un corps donné (en fixant δ) et étudier son passage au méridien en fonction des latitudes.