
Passage d'un astre au méridien inférieur |
Par définition, à l'instant du passage au méridien inférieur, l'angle horaire est égale à 180° (H = 180°).
Les équations ci-dessous montrent qu'on a donc deux solutions :
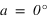 et
et 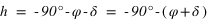 équation (3)
équation (3)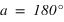 et
et 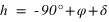 équation (4)
équation (4)
Avec toujours la condition supplémentaire : 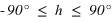 . On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si
. On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si 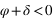 donc si
donc si 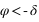 . Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si
. Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si 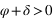 donc si
donc si 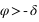 . Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors
. Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors 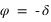 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.
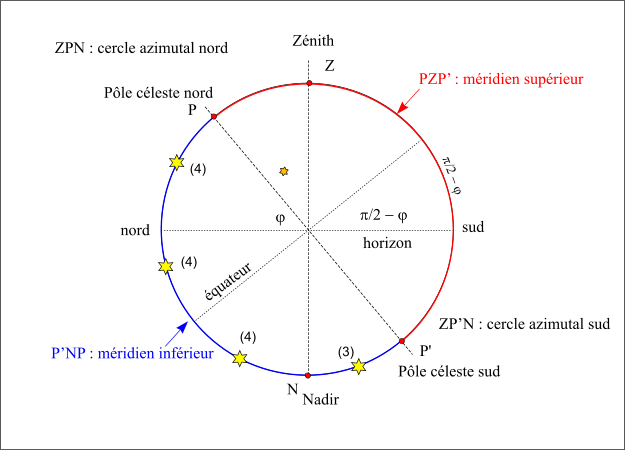
Sur la figure, on a fait une coupe méridienne de la sphère céleste. Le méridien inférieur est représenté en bleu c’est le demi-cercle PNP’. L’étoile notée (3) passe au méridien inférieur avec un azimut nord (elle est sur l’arc ZP’N), sa hauteur est comptée à partir de la direction sud de l’horizon. Les autres étoiles, notées (4), passent au méridien inférieur avec un azimut nord (elles sont sur l’arc ZPN) leurs hauteurs sont comptées à partir de la direction nord de l’horizon ; une passe au dessus de l’horizon, car une partie du méridien inférieur est au-dessus de l’horizon (nord -P), les deux autres passent sous l’horizon.
Les équations de transformation de coordonnées donnent :
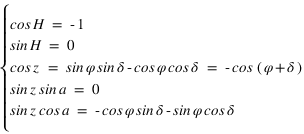
si 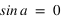 alors
alors 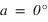 ou
ou 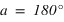 . Si
. Si 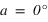 alors
alors 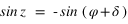 et si
et si 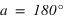 alors
alors 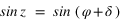 .
.