
|
Les formulaires de changement de repères en coordonnées polaires font appel à la trigonométrie sphérique. Pour cela nous allons utiliser les formules de trigonométriques sphériques classiques.
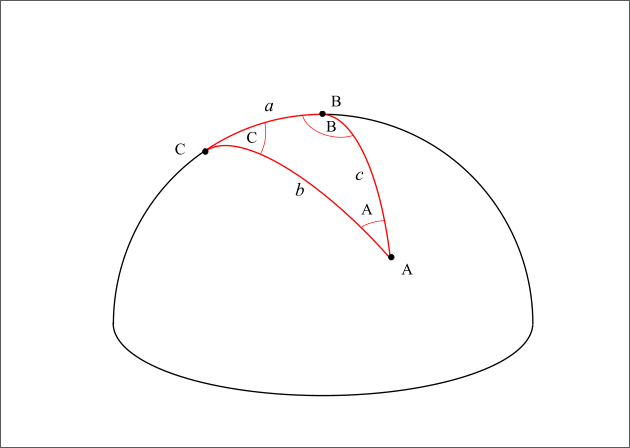
Considérons un triangle sphérique ABC formé par des arcs de grands cercles de la sphère, ce triangle possède trois angles aux sommets A, B et C et trois angles « côtés » a, b, c. A, B et C sont les angles entre les arcs de grands cercles et a, b et c sont les longueurs angulaires des arcs de grands cercles. Entre ces six angles, on a les relations trigonométriques suivantes :
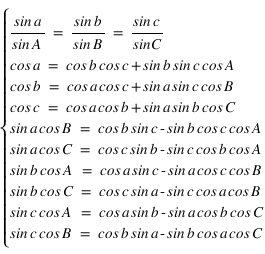
Il est inutile de connaître ces formules par cœur, il suffit de savoir qu’elles existent et de s’y rapporter lorsque l’on a un calcul à faire.