Relations entre les coordonnées polaires écliptiques et équatoriales

Si l’on trace les deux repères sur la sphère céleste et un astre quelconque en A, le pôle de l’écliptique P_E, le pôle nord céleste P et la direction de l’astre A forme un triangle sphérique (P_EPA).

Triangle sphérique, repères écliptique et équatorial.

Figure 12 : Triangle sphérique, repères écliptique et équatorial.

Crédit : ASM/Patrick Rocher

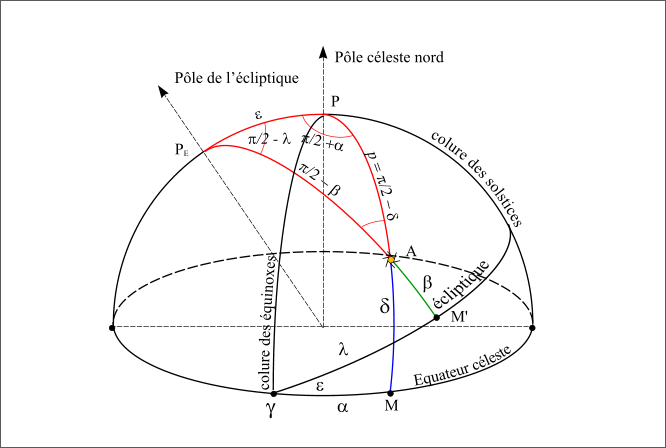
Dans ce triangle on connait cinq des six angles :

L’arc P_EP est l’obliquité ε,
L’arc P_EA est le complémentaire de la latitude écliptique : ,
L’arc PA est la distance polaire ou le complémentaire de la déclinaison :,
L’angle entre l’arc P_EP et l’arc P_EA est le complémentaire de la longitude écliptique :,
L’angle entre P_EP et PA est égal à 90° (π/2) l’angle entre les deux colures plus l’ascension droite de l’astre :.

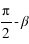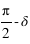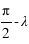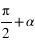Pour avoir par exemple les coordonnées équatoriales en fonction des coordonnées écliptiques, il suffit d’écrire les relations suivantes :

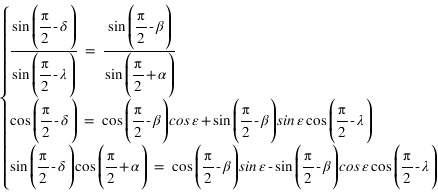
système(sin(pi/2-delta)/sin(pi/2-lambda)=sin(pi/2-beta)/sin(pi/2+alpha);cos(pi/2-delta)=cos(pi/2-beta)*cos*epsilon +sin(pi/2-beta)*sin*epsilon*cos(pi/2-lambda);sin(pi/2-delta)*cos(pi/2+alpha)=cos(pi/2-beta)*sin*epsilon -sin(pi/2-beta)*cos*epsilon*cos(pi/2-lambda))

Ce qui donne après simplification :

Système (1) 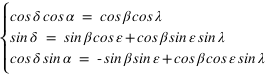système(cos*delta*cos*alpha=cos*beta*cos*lambda;sin*delta=sin*beta*cos*epsilon+cos*beta*sin*epsilon*sin*lambda;cos*delta*sin*alpha=-sin*beta*sin*epsilon+cos*beta*cos*epsilon*sin*lambda)

La déclinaison s’obtient à l’aide de la seconde relation en prenant l’arc sinus de sin δ (car δ est compris en –90° et +90°) l’ascension droite est obtenue grâce à la première et à la troisième relation. La connaissance du sinus et du cosinus de l’ascension droite permet de connaître l’ascension droite sur l’intervalle allant de 0° à 360°. On doit ensuite mettre ces deux variables dans le bon système d’unités (heures sexagésimales pour l’ascension droite et degrés sexagésimaux pour la déclinaison).

On a des relations identiques pour passer des coordonnées équatoriales aux coordonnées écliptiques.

Système (2) 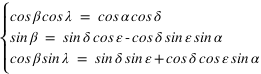système(cos*beta*cos*lambda=cos*alpha*cos*delta;sin*beta=sin*delta*cos*epsilon-cos*delta*sin*epsilon*sin*alpha;cos*beta*sin*lambda=sin*delta*sin*epsilon+cos*delta*cos*epsilon*sin*alpha)

Auteur: ASM/Patrick Rocher

Calcul des coordonnées équatoriales du Soleil

Cet exercice a pour but de vous faire calculer les coordonnées équatoriales du Soleil à partir de ces coordonnées écliptiques. Pour simplifier, le calcul on supposera que la latitude du Soleil β est nulle, ce qui implique que 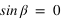sin*beta=0 et que 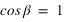cos*beta=1 . Le système (1) est donc simplifié.

Question 1)

Le 1 janvier 2012 à 0h UTC, la longitude apparente λ du Soleil est de 279° 57' 30", calculer son ascension droite et sa déclinaison sachant que l'obliquité de l'écliptique ε à cet instant est de 23°26' 12,7". On exprimera l'ascension droite en heures, minutes et secondes d'angle et la déclinaison en dégres, minutes et secondes d'angle.

Aide