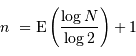Plus de dix ordres de grandeurs séparent les énergies des photons
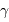 à radio auxquels s'intéressent les astrophysiciens. Les techniques de détection, tout comme les
détecteurs, sont évidemment bien différentes selon le domaine spectral.
à radio auxquels s'intéressent les astrophysiciens. Les techniques de détection, tout comme les
détecteurs, sont évidemment bien différentes selon le domaine spectral.
Cette section présente des caractéristiques générales, et explore préférentiellement le domaine spectral visible ainsi que les domaines proches du visibles où les détecteurs présentent des propriétés semblables.
Une section est spécialement dédiée aux détecteurs CCD et aux observations avec une caméra CCD. Une autre s'intéresse aux observations dans l'infrarouge thermique.
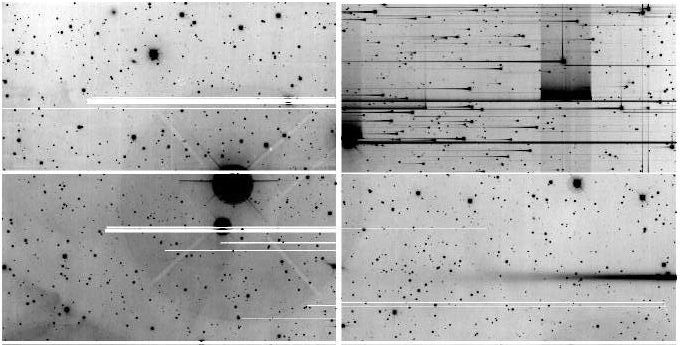
Fragment d'image, brute, obtenue par la caméra CFH12k du télescope
CFH
Crédit :
CFHT
Réponse spectrale
La réponse spectrale d'un détecteur indique son rendement en fonction de la longueur d'onde. Sans l'instrumentation appropriée, un détecteur ne fournit pas d'information sur la couleur précise d'un photon détecté.
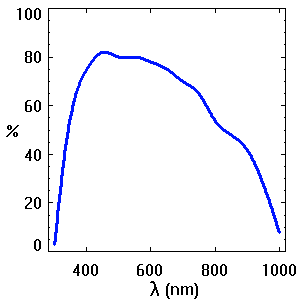
Réponse spectrale d'un CCD éclairé par l'arrière. Un tel détecteur ne voit ni les photons UV ni les photons IR. Il n'est pas non plus capable de distinguer un photon rouge d'un photon bleu s'il n'est pas précédé de l'instrumentation appropriée (filtre ou spectrographe).
Crédit :
ASM
Pixels
La taille et le nombre des pixels est un paramètre important. Une photodiode est monopixel ; les mosaïque CCD pour l'astronomie peuvent compter jusqu'à 2k 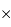 4k pixels, les plus grands CCD actuels (2003) atteignant la taille 8k
4k pixels, les plus grands CCD actuels (2003) atteignant la taille 8k 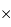 8k pixels.
8k pixels.

La résolution atteinte sur cet objet du voisinage de NGC3486, observé en bande B et I dans des conditions de
seeing de 0.7", met clairement en évidence la pixélisation de la caméra grand champ.
Crédit :
CFHT
Saturation
Exemple de détecteur saturé, en raison d'une trop grande dynamique entre les signaux à enregistrer. La saturation conduit à élargir démesurément la tache image, car les trop nombreux photo-électrons ont débordé du puits de potentiel où ils auraient dû être stockés.

Système binaire Gliese 229. La composante Gb299A est totalement saturée, pour mettre en évidence le compagnon Gl229B, de masse substellaire, qui est une
naine brune.
Crédit :
HST
Propriétés d'un détecteur
On peut synthétiser les propriétés d'un détecteur selon différentes caractéristiques, chacune associée à une dimension physique particulière.
Les principales caractéristiques sont traitées avec plus de détail dans des pages dédiées.
Caractéristiques
Exemple de caractéristiques d'un détecteur : mosaïque de la caméra CFH12k du télescope CFH.

Détecteurs
On peut distinguer 3 grands type de détection :
- Détection quantique :
Un photon incident, absorbé, conduit à l'apparition d'un porteur de charges.
- Détection cohérente : Les récepteurs d'amplitude sont
sensibles à l'amplitude et à la phase du signal électromagnétique.
Le collecteur est dans ce cas souvent appelé antenne. La détection
cohérente nécessite, dans les plus hautes fréquences auxquelles
elle peut être menée, le mélange du signal scientifique et d'un
signal de référence. La création d'un signal de référence stable,
cohérent, n'est technologiquement réalisable qu'aux basses
fréquences, en pratique pour les signaux de fréquence
inférieure à 1500 GHz (longueur d'onde de 200 micromètres).
- Détection thermique : Un bolomètre absorbe l'énergie du
rayonnement incident et la dégrade en agitation thermique.
L'élévation thermique qui en résulte est mesurée par la variation
d'une grandeur physique reliée à la température.
 Principe de la détection hétérodyne
Principe de la détection hétérodyne
Difficulté : ☆
Temps : 15 min
La détection hétérodyne compare le signal scientifique à un signal de référence délivré par un oscillateur local à haute fréquence. On note 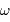 la pulsation du signal scientifique, et
la pulsation du signal scientifique, et 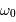 celle de la référence, cette dernière étant voisine de
celle de la référence, cette dernière étant voisine de 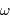 .
.
Question 1)
Un mélangeur fournit le signal produit des signaux observé et de référence.
Montrer que ce signal est composé de 2 fréquences bien distinctes.
On rappelle :
![\cos a \cos b = {1\over 2} \Bigl[ \cos (a+b) + \cos (a-b) \Bigr]](../pages_detecter/equations_detection-physique/equation7.png)
Question 2)
On applique au signal un filtre passe-bas, pour éliminer les hautes fréquences.
Montrer l'intérêt du mélange des signaux.
Que reste-t-il du signal précédent après élimination des hautes fréquences ?
 Objectifs
Objectifs
Illustrer comment l'interaction matière-rayonnement permet de
transférer l'information utile d'un photon à un photo-électron.
Photo-électron
L'absorption d'un photon permet à un électron du détecteur de
changer d'état. Cette création d'un photo-électron par absorption
d'un photon caractérise les détecteurs quantiques.
Du signal lumineux au signal enregistrable
La conversion photon + électron 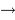 photo-électron s'appuie sur différents effets.
photo-électron s'appuie sur différents effets.
| Effet | Description | Récepteur |
| Effet photochimique | Changement d'état chimique | Plaques photo, plus guère employées aujourd'hui. Les photo-électrons activés par le rayonnement réduisent les ions Ag+ en argent métallique. |
| Effet photoélectrique | Extraction d'un électron d'un métal vers le vide | Phototube, photomultiplicateur |
| Effet photoconducteur | Au sein d'un semi-conducteur, l'absorption d'un photon permet à un électron de franchir le gap de la bande de valence vers la bande de conduction | Photodiode |
| Effet photovoltaïque | Effet photoconducteur dans une jonction PN.
Un photon crée une paire
électron-trou, qui se traduit pas une différence de potentiel
aux bornes de la jonction ;
IR lointain 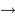 radio radio
| |
Linéarité
On demande à une mesure physique de fournir une mesure en liaison avec l'observable voulue. Une propriété importante est la linéarité : si elle n'est pas assurée, la relation entre le signal mesuré et le signal observé est complexe.
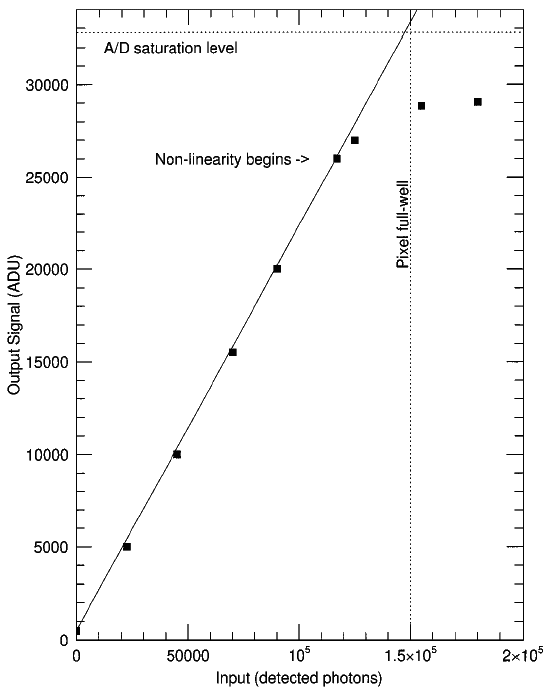
Courbe de linéarité typique d'une caméra CCD. Ici, la linéarité est assurée d'environ 500 à 25000 ADU (unités de signal numérisé), puis le détecteur sature.
Crédit :
CFHT
Seuil et saturation
L'effet de seuil peut introduire un décalage sur une faible mesure. Le niveau de signal doit être suffisant pour sortir du bruit propre du détecteur. A faible niveau, la définition du signal nul (offset) peut également affecter le signal. La saturation affecte les fortes valeurs de signal.
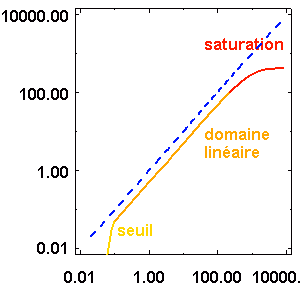
L'excitation est en abscisse, la réponse en ordonnée (échelle log-log). La ligne tiretée en bleu donne une réponse idéale, identique à l'excitation, sans seuil ni saturation, de rendement unité. En deçà du seuil, la réponse d'un détecteur réel est mauvaise ; au-delà d'une certaine valeur, le détecteur sature.
Noter que le rendement n'est pas 1.
Crédit :
ASM
 Objectifs
Objectifs
Un bon détecteur est linéaire sur une grande dynamique, et propose un seuil de sensibilité bas.
Seuil de sensibilité
Un récepteur sera d'autant plus sensible que... son seuil de sensibilité est bas. Ceci nécessite le plus souvent son refroidissement, afin de diminuer le bruit d'agitation thermique.
Linéarité
La linéarité assure une réponse proportionnelle au signal incident.
C'est une propriété importante pour convertir une observable en mesure. Si le détecteur est linéaire, il est possible par un simple facteur d'échelle de convertir le signal électrique enregistré en signal photométrique.
Saturation
La saturation limite le flux maximum observable. Un niveau de saturation élevé assure une grande dynamique.
Réponse spectrale d'un CCD
La réponse spectrale d'un CCD dépend du matériau semi-conducteur utilisé et des caractéristiques géométriques du sandwich de détection.
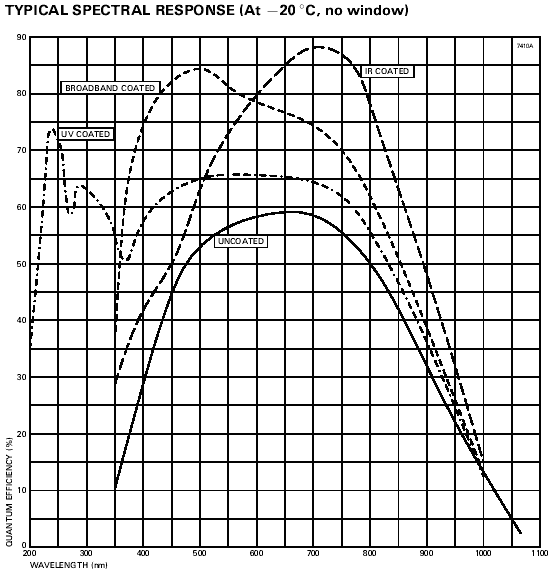
Réponse spectrale d'un CCD, selon le traitement de surface (=coating), optimisé vers l'IR, l'UV, ou bien plus une plus grande bande spectrale visible. CCD30-11 de Marconi Applied Technologies
Crédit :
Marconi
Réponse spectrale d'un bolomètre pour la radioastronomie
Un bolomètre ne discrimine pas les longueurs d'onde... mais cela ne signifie pas qu'il est également sensible à toutes les longueurs d'onde. Le signal délivré est en fait intégré selon une fenêtre spectrale donnée.
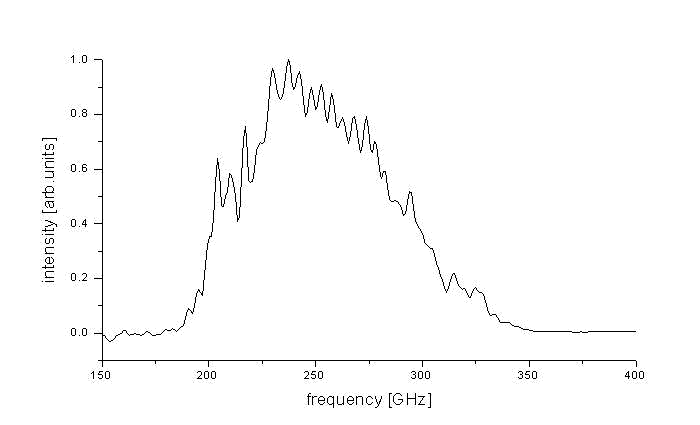
Courbe de réponse spectrale de l'instrument Mambo de l'
IRAM (Max Planck Millimetre Bolometer).
Crédit :
IRAM
Sensibilité spectrale
Un détecteur n'est sensible que dans une gamme spectrale donnée. Il n'a en général aucune sélectivité spectrale intrinsèque, sauf s'il est muni de filtre adéquat.
Résolution spectrale
De ce qui précède, on déduit que la résolution spectrale dépend essentiellement des filtres ou de l'instrumentation associés au détecteur.

Fréquence de lecture d'une caméra CCD. Plus elle est rapide, plus le bruit de lecture augmente.
Crédit :
ANDOR technologies
Réponse temporelle
La rapidité de lecture d'un CCD dépend de la fréquence d'horloge de l'électronique et du nombre de pixel. Le fait de n'avoir qu'un nombre de registre de lecture limité (1 à 4 typiquement) ralentit considérablement la réponse temporelle d'un détecteur composé de millions de pixels.

Obturateur géant (1 m) de la caméra Megacam du CFHT.
Crédit :
CEA/CFHT
Obturateur
Un obturateur mécanique est souvent nécessaire pour stopper l'arrivée des photons durant le temps de lecture de la caméra. Dans certains cas, cet élément peut limiter la cadence d'observation.
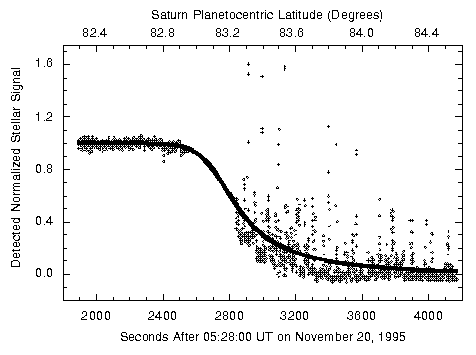
La réponse temporelle devient un paramètre important pour l'observation d'un phénomène rapidement variable. Ici : occultation d'une étoile brillante par
Saturne.
Crédit :
NASA/IRTF
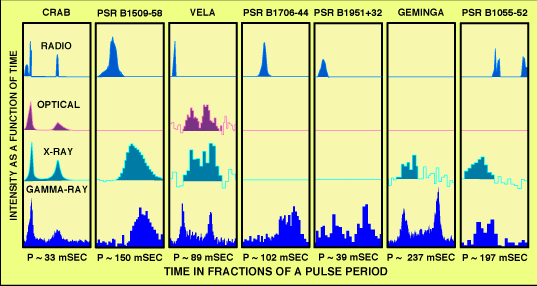

Variations temporelles d'un signal émis par un pulsar. Echantillonner un signal très rapide est souvent orthogonal aux capacités d'imagerie : le détecteur le plus rapide sera mono-pixel.
Crédit :
NASA/CGRO (Compton Gamma Ray Observatory)
De la nécessité d'observer avec une bonne cadence
L'observation astronomique se caractérise souvent par des poses très longues, nécessaires pour l'obtention d'un signal intrinsèquement très faible. Mais il est aussi utile de pouvoir compter sur des détecteurs rapides.
La réponse temporelle prend son importance pour l'observation d'un phénomène périodique rapide, comme p.ex. le clignotement d'un pulsar, ou pour un phénomène transitoire, tel une occultation stellaire.
Temps de réponse, temps de lecture
Un détecteur a un temps de réponse, propre ou dépendant de l'électronique de contrôle et de lecture, qui n'est pas infiniment bref.
Par exemple, un bolomètre, qui convertit l'énergie des photons en échauffement, ne peut pas réponde instantanément. De même que la lecture d'une matrice CCD de plusieurs millions de pixels ne peut pas être instantanée, mais prendra jusqu'à une minute.
Il s'ensuit que le signal d'un détecteur est échantillonné dans le temps.
Filtrage
De ce qui précède, on en déduit qu'un détecteur fonctionne comme un filtre passe-bas : les hautes fréquences temporelles sont filtrées.
Pose longue ou échantillonnage rapide
Certains phénomènes astronomiques présentent de rapides variations temporelles, soit parce qu'intrinsèquement variables, soit parce que correspondant à un phénomène transitoire. L'observation de tels phénomènes demande un temps de réponse rapide, et donc une stratégie de détection appropriée.
 Temps de réponse
Temps de réponse
Difficulté : ☆
Temps : 10 min
Une observation astérosismique avec le spectromètre HARPS nécessite
la lecture d'une caméra de 2k×4k. Par ailleurs, l'échantillonnage du signal temporel nécessite l'acquisition d'une image par minute.
Question 1)
Déterminer le temps de pose en fonction de la magnitude, sachant que le détecteur sature à partir de 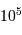 photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
Rappel : magnitude et luminosité varient dans le rapport :
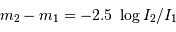
Question 2)
Le temps de lecture de la caméra est de 20 s. Pour quelle magnitude minimale l'observation reste-t-elle pertinente, avec au-moins la moitié du temps passée sur la source et non à lire la caméra ?
Question 3)
L'observation demande un échantillonnage plus rapide que 3 minutes. Montrer qu'une cible peu brillante ne sera pas observée dans de bonnes conditions. Estimer la limite en magnitude dans le cas où l'on accepte de remplir les pixels à 1/10 de la valeur optimale.
La pose sur l'objet est nécessairement limitée à 160 s.
Format
Les CCD actuels pour l'astronomie ont des tailles limitées à 2k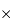 4k.
Pour augmenter la capacité de détection, on pave le plan focal de plusieurs détecteurs, comme par exemple pour la caméra MEGACAM du télescope CFH mise en service à l'été 2003.
4k.
Pour augmenter la capacité de détection, on pave le plan focal de plusieurs détecteurs, comme par exemple pour la caméra MEGACAM du télescope CFH mise en service à l'été 2003.

Les 40 CCD de la caméra MEGACAM du télescope
CFH.
Crédit :
CFHT
Pixel
 Définition
Définition
Un pixel, pour picture element, est un élément d'image. Par
extension, un pixel d'une caméra CCD correspond à l'entité
physique qui aboutit à un élément d'image.
Le nombre de pixels court de 1 à plusieurs millions ; on note couramment
1 kpx = 1000 px.
Format
Les caméras actuelles ont typiquement des formats de 256  256 px (dans l'infrarouge thermique) à 2k
256 px (dans l'infrarouge thermique) à 2k  4k pixels (dans le visible).
4k pixels (dans le visible).
Le format est la seule caractéristique où la détection par plaque photographique fut plus performante. Les détecteurs de type CCD comptent un nombre de pixels bien inférieur à celui atteint par les plus grandes plaques photos.
 Projet MEGACAM du télescope CFH
Projet MEGACAM du télescope CFH
Difficulté : ☆
Temps : 10 min

Champ plat des 40 CCD de la caméra MEGACAM du
CFH
Crédit :
CFHT
La caméra MEGACAM du télescope CFH, mise en service à l'été 2003, comprend
40 mosaïques CCD, de 2k  4.5k pixels. L'information d'un pixel est codé sur 16 bits. Le temps de lecture d'une image totale est de 30 secondes.
4.5k pixels. L'information d'un pixel est codé sur 16 bits. Le temps de lecture d'une image totale est de 30 secondes.
Question 1)
Les 36 CCD centraux, couvrent une surface carrée de 0.94 degré par 0.94 degré. Déterminer le champ de vue d'un pixel.
Déterminer le nombre total de pixels pour 36 CCD.
Question 2)
Déterminer la capacité de stockage nécessaire pour 1 champ observé en 3 couleurs.
1 pixel codé sur 16 bits nécessite 2 octets pour le stockage.
Question 3)
Une nuit moyenne aboutit à une dizaine de champs, chacun pris dans 3 filtres.
A raison de 100 nuits d'observation par an, déterminer le volume de données au bout de 5 années de fonctionnement.
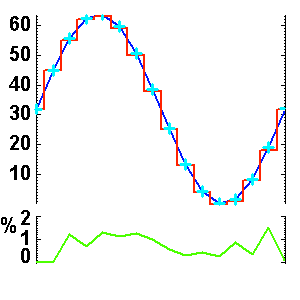
Signal analogique et numérisé sur 8 bits (64 valeurs possibles). La différence entre les valeurs réelles et codées introduit un
bruit de numérisation.
Crédit :
ASM
Bruit de numérisation
Le simple fait de numériser un signal analogique, càd de le coder sur une échelle de valeurs discrétisée (typiquement, sur 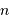 bits, ce qui permet de coder
bits, ce qui permet de coder 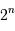 valeurs), peut rajouter du bruit au signal.
valeurs), peut rajouter du bruit au signal.
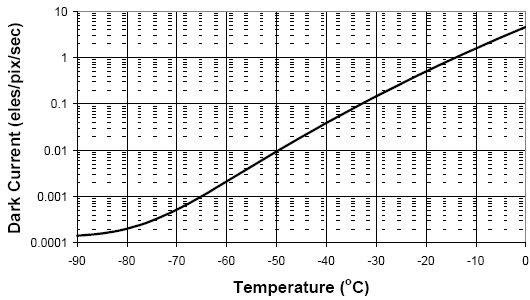
Le signal d'obscurité est un bruit d'origine thermique. Données pour une caméra CCD, en fontions de la température. A -15 deg, 1 électron thermique est généré par pixel par seconde ; à -65 deg, il faut attendre 1000 s pour qu'un moyenne un électron thermique apparaisse par pixel.
Crédit :
ANDOR
Bruit d'origine thermique
La température du détecteur conditionne le signal d'obscurité d'un détecteur. Suite à l'agitation thermique, des porteurs de charge apparaissent aléatoirement, d'autant plus que la température est élevée.
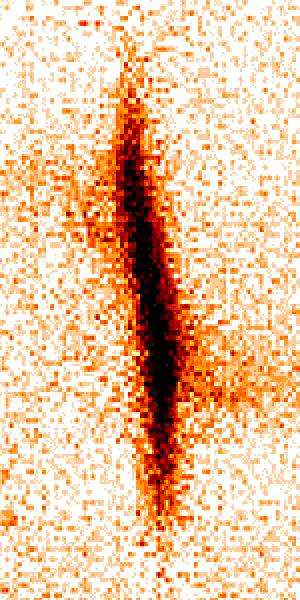
Bruit de fond
Crédit :
ESO
Signaux parasites et bruits
Au signal scientifique se superposent des signaux parasites et des bruits.
Un bruit sera caractérisé par son caractère aléatoire, et les propriétés statistiques correspondantes.
Un signal parasite possède, comme son nom l'indique, les propriétés d'un signal et non celles d'un bruit.
Bruit quantique
La nature du rayonnement, quantique par excellence, montre le hiatus à décrire une intensité lumineuse par une quantité analogique, alors que les porteurs de ce rayonnement sont quantifiés.
On montre que la
statistique d'arrivée des photons est poissonnienne.
Lorsque l'on attend 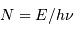 photons, la valeur moyenne
observée est
photons, la valeur moyenne
observée est 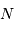 et la fluctuation
et la fluctuation 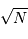 autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
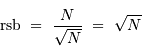
En électronique, on parle de bruit de grenaille, et de bruit de
photons en optique.
Bruit de fond
Le bruit de fond représente le bruit de photons de la lumière parasite qui se superpose au signal scientifique. Comme le bruit quantique, il est lié aux sources (ici parasites) et non au détecteur. Dans l'infrarouge, il est dominé par l'environnement chaud que voit le détecteur.
Bruit thermique
Le bruit thermique provient de l'agitation thermique des porteurs de charge du détecteur. Il est à moyenne nulle, son écart-type augmente avec la température.
Ce bruit, comme les suivants, dépend du détecteur et de la chaîne de détection.
Bruit de lecture
Le processus de lecture contribue au bruit de lecture, par exemple dans un CCD lorsque les photo-électrons sont transférés le long d'une colonne vers un registre de lecture.
On quantifie le bruit de lecture par son écart-type en nombre de photoélectrons par pixel. Une valeur typique de 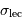 est de l'ordre de quelques photo-électrons par pixel
est de l'ordre de quelques photo-électrons par pixel
Bruit d'amplification
L'électronique d'amplification introduit un gain 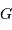 , dont la valeur n'est pas fixe mais sujette à différents bruits.
, dont la valeur n'est pas fixe mais sujette à différents bruits.
 Numérisation
Numérisation
Difficulté : ☆
Temps : 15 min
On souhaite numériser le signal photométrique d'un détecteur dédié à une étude de la microvariabilité. Ce signal est composé d'un fort continu, de diverses modulations et bruit, et du signal scientifique. Les amplitudes respectives sont données dans le tableau ci-dessous.
| continu | 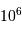 |
| variations | 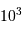 |
| microvariabilité | 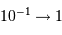 |
Question 1)
Sans traitement préalable, sur combien de bits faut-il coder le signal afin de ne pas introduire de bruit lors de cette opération (si besoin, voir les pages sur
l'échantillonnage d'un signal) ?
L'échantillonnage du signal requiert de coder le niveau de signal à la moitié de la plus petite variation.
Déterminer l'amplitude relative du signal entre le niveau de codage et la valeur maximale
Question 2)
Même question, après filtrage permettant de séparer les composantes continue et lentement variable d'une part, et la microvariabilité se distinguant du fond variable de l'autre.
Même démarche que précédemment.
Diverses contributions au rendement
Lorsque l'on décompte toutes les pertes de transmission des différents éléments d'une chaîne instrumentale, on s'aperçoit que le rendement final n'est pas nécessairement bon. Pour 100 photons collectables au sommet de l'atmosphère, la plupart des instruments ne travailleront finalement qu'avec une poignée de photoélectrons.
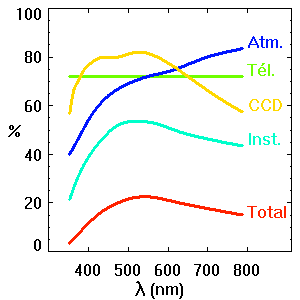
Transmissions des différentes contributions d'une chaîne instrumentale : l'atmosphère (au niveau de la mer, pour une observation au zénith), du télescope, de l'instrument, du détecteur CCD, et finalement transmission totale.
Crédit :
ASM
Choix d'un site
On peut considérer comme partie intégrante du rendement celui de la couverture temporelle durant laquelle la météo est favorable. L'image satellite illustre le fait que le Chili offre de bien meilleurs sites d'observations que l'Argentine, avec un ciel parfaitement dégagé.

Image satellite de l'Amérique du Sud, dans la fenêtre à 10 micromètres, sensible à la couverture nuageuse. Les courants froids du Pacifique Sud sont responsables du faible taux moyen d'humidité au Chili. Les bons sites comme dans la Cordillère des Andes au Chili offrent plus de 300 nuits claires par an.
Crédit :
GEOS
Rendement de la chaîne de détection
Lorsque les photons sont rares, pour des sources faiblement lumineuses, il faut viser l'efficacité lors de chacune des étapes participant à la chaîne de mesure, et ce bien avant le détecteur.
- Atmosphère :
La transmission atmosphérique dépend de la longueur d'onde et de la quantité d'atmosphère traversée (sauf pour une observation spatiale).
- Collecteur :
L'efficacité de la collection dépend du pouvoir de réflexion des miroirs. En fonction de la longueur d'onde et du traitement de surface adapté (aluminure, argenture, dorure...), le facteur de réflexion d'un miroir vaut typiquement entre 80 et 99%.
- Instruments :
Un instrument efficace n'égare pas ses photons. Mais chaque dioptre, traversées vitreuses (lentilles...), chaque passage par fibre optique... épluche les photons par réflexion, transmission, absorption.
- Détecteur :
Le rendement du détecteur est la dernière étape limitant le rendement global de la chaine de détection.
Transmissions
Valeurs typiques de transmission de différentes composantes d'une chaîne de mesure
| atmosphère | 60 à 80%, dépend de la masse d'air (mesure la quantité d'atmosphère traversée, càd 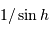 , avec , avec 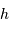 la hauteur sur l'horizon de l'objet visé) la hauteur sur l'horizon de l'objet visé) |
| miroir | jusqu'à 99%, en fonction du traitement réfléchissant de surface |
| fibre | de l'ordre de 80% |
| dioptre | une réflexion verre-air a un coefficient de transmission typiquement de 96%. Un traitement antireflet permet d'accroître ce coefficient jusque vers 99% |
 De l'intérêt d'un traitement de surface
De l'intérêt d'un traitement de surface
Difficulté : ☆
Temps : 5 min
Question 1)
Un instrument comprend en tout 10 lentilles. Sans traitement antireflet, chaque dioptre a une transmission de 96%.
Déterminer la transmission globale.
[2 points]
Question 2)
Un traitement antireflet permet de porter le coefficient de transmission à 99%. Que devient la transmission globale ?
[1 points]
Question 3)
Conclure.
[1 points]
 Transmission atmosphérique
Transmission atmosphérique
Difficulté : ☆
Temps : 15 min
Les données de l'appliquette ci-jointe montrent l'évolution de la transmission atmosphérique avec la longueur dans le domaine visible, pour 2 altitudes d'observation : au niveau de la mer et au sommet du Mauna Kea (Hawaï, 4200 m d'altitude).

Question 1)
Tracer, pour les 2 altitudes d'observation, les transmissions en fonction de la longueur d'onde, et commenter l'allure des courbes.
[2 points]
Question 2)
La relation de l'extinction avec la masse d'air de l'objet visé 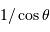 , l'angle
, l'angle 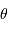 mesurant la distance angulaire entre le zénith et la direction de visée, est de la forme :
mesurant la distance angulaire entre le zénith et la direction de visée, est de la forme :
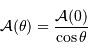
Commenter et justifier cette relation.
[1 points]
Faire un schéma montrant les couches d'atmosphère traversées avant la détection.
Question 3)
Montrer, en calculant l'extinction au CFH, que la courbe d'extinction est compatible avec la diffusion Rayleigh, qui varie comme l'inverse de la puissance quatrième de la longueur d'onde
[1 points]
Dans l'appliquette :
- sélectionner la 1ère case de la colonne 1-T (D1) et réaliser :
=100-C1
- sélectionner la 1ère case de la colonne (lambda^-4) (E1) et réaliser :
=(1000/A1)^4
Pour en savoir plus sur les thématiques de cette section ; voir
p.ex. le livre Méthodes physiques de l'observation, de
Pierre Léna, CNRS éditions.
Crédit :
ASM
- Question 1
Aide :
Rappel : magnitude et luminosité varient dans le rapport :
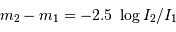
Solution :
Par application de la définition de la magnitude, le flux d'une étoile de magnitude 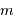 vaut
vaut 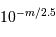 par rapport à celui d'une étoile de magnitude nulle.
par rapport à celui d'une étoile de magnitude nulle.
Le temps de pose étant limité par le flux optimal sur un pixel, une pose de durée 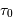 pour une magnitude nulle sera multipliée par
pour une magnitude nulle sera multipliée par 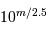 pour une magnitude
pour une magnitude 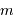 .
.
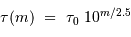
Soit 10 s pour une magnitude 2.5, 100 s pour une magnitude 5.
- Question 2
Solution :
En application de ce qui précède, une pose de 20 s correspond à la magnitude 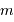 vérifiant
vérifiant
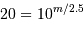 , càd
, càd 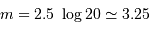 .
.
Le temps de pose pour une étoile plus brillante que la magnitude 3.25 est plus court que 20 s : le temps est majoritairement dépensé à lire le détecteur.
- Question 3
Aide :
La pose sur l'objet est nécessairement limitée à 160 s.
Solution :
En application de ce qui précède (avec des pixels bien remplis), une pose de 160 s correspond à la magnitude 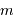 vérifiant
vérifiant
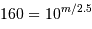 , càd
, càd 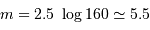 .
.
Le temps de pose pour une étoile moins brillante que la magnitude 5.5 dépasse 160 s.
En acceptant de remplir les pixels de façon très incomplète, le gain d'un facteur 10 en nombre de photoélectrons, donc de photons, correspond à un surcroît de 2.5 magnitudes. La limite en magnitude est donc de l'ordre de 8.
 à radio auxquels s'intéressent les astrophysiciens. Les techniques de détection, tout comme les
détecteurs, sont évidemment bien différentes selon le domaine spectral.
à radio auxquels s'intéressent les astrophysiciens. Les techniques de détection, tout comme les
détecteurs, sont évidemment bien différentes selon le domaine spectral.


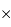 4k pixels, les plus grands CCD actuels (2003) atteignant la taille 8k
4k pixels, les plus grands CCD actuels (2003) atteignant la taille 8k 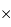 8k pixels.
8k pixels.


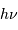 alors
qu'un détecteur cohérent voir le champ électromagnétique,
alors
qu'un détecteur cohérent voir le champ électromagnétique,
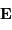 ou
ou 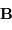 .
.
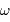 la pulsation du signal scientifique, et
la pulsation du signal scientifique, et 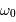 celle de la référence, cette dernière étant voisine de
celle de la référence, cette dernière étant voisine de 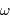 .
.
![\cos a \cos b = {1\over 2} \Bigl[ \cos (a+b) + \cos (a-b) \Bigr]](../pages_detecter/equations_detection-physique/equation7.png)
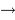 photo-électron s'appuie sur différents effets.
photo-électron s'appuie sur différents effets.
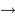 radio
radio
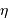 de création d'un photoélectron, souvent
appelée rendement quantique, dépend de différents paramètres, et
varie fortement avec la longueur d'onde :
de création d'un photoélectron, souvent
appelée rendement quantique, dépend de différents paramètres, et
varie fortement avec la longueur d'onde :
![\eta (\lambda) \ = \ (1-r) \ \varepsilon\ \bigl[1-\exp(-\alpha_\lambda \ell)\bigr]](../pages_detecter/equations_detection-quantique/equation4.png)
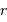
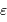
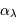
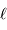
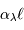 augmente, plus la probabilité d'absorption d'un photon est grande
augmente, plus la probabilité d'absorption d'un photon est grande








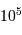 photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
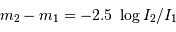
 4k.
Pour augmenter la capacité de détection, on pave le plan focal de plusieurs détecteurs, comme par exemple pour la
4k.
Pour augmenter la capacité de détection, on pave le plan focal de plusieurs détecteurs, comme par exemple pour la 
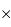 256 px (dans l'infrarouge thermique) à 2k
256 px (dans l'infrarouge thermique) à 2k 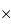 4k pixels (dans le visible).
4k pixels (dans le visible).

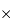 4.5k pixels. L'information d'un pixel est codé sur 16 bits. Le temps de lecture d'une image totale est de 30 secondes.
4.5k pixels. L'information d'un pixel est codé sur 16 bits. Le temps de lecture d'une image totale est de 30 secondes.

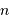 bits, ce qui permet de coder
bits, ce qui permet de coder 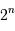 valeurs), peut rajouter du bruit au signal.
valeurs), peut rajouter du bruit au signal.


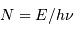 photons, la valeur moyenne
observée est
photons, la valeur moyenne
observée est 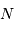 et la fluctuation
et la fluctuation 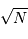 autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
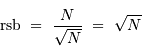
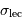 est de l'ordre de quelques photo-électrons par pixel
est de l'ordre de quelques photo-électrons par pixel
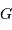 , dont la valeur n'est pas fixe mais sujette à différents bruits.
, dont la valeur n'est pas fixe mais sujette à différents bruits.
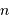 éléments d'information (bit), ce qui permet uniquement
éléments d'information (bit), ce qui permet uniquement 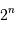 valeurs de codage.
valeurs de codage.
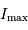 présentera, de par le codage sur
présentera, de par le codage sur 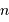 éléments d'information, une résolution minimale de
éléments d'information, une résolution minimale de 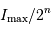 .
.
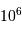
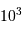
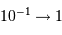


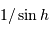 , avec
, avec 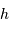 la hauteur sur l'horizon de l'objet visé)
la hauteur sur l'horizon de l'objet visé) 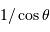 , l'angle
, l'angle 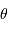 mesurant la distance angulaire entre le zénith et la direction de visée, est de la forme :
mesurant la distance angulaire entre le zénith et la direction de visée, est de la forme :
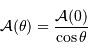

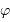 le déphasage inconnu à un instant de référence choisi comme origine, le produit des signaux est proportionnel à :
le déphasage inconnu à un instant de référence choisi comme origine, le produit des signaux est proportionnel à :
![\cos( \omega t +\varphi) \cos \omega_0 t = {1\over 2} \left[ \cos \bigl( (\omega+\omega_0) t + \varphi \bigr) + \cos \bigl( (\omega-\omega_0)t-\varphi \bigr) \right]](../pages_detecter/equations_detection-physique/equation9.png)
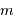 vaut
vaut 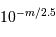 par rapport à celui d'une étoile de magnitude nulle.
par rapport à celui d'une étoile de magnitude nulle.
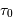 pour une magnitude nulle sera multipliée par
pour une magnitude nulle sera multipliée par 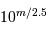 pour une magnitude
pour une magnitude 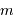 .
.
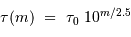
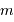 vérifiant
vérifiant
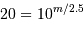 , càd
, càd 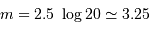 .
.
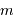 vérifiant
vérifiant
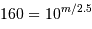 , càd
, càd 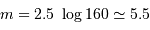 .
.
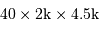 , soit 360 Mpx, d'où un taille de 720 Mo par image.
, soit 360 Mpx, d'où un taille de 720 Mo par image.
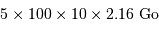 , soit 10.8 téraoctets.
, soit 10.8 téraoctets.
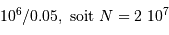 .
.