 |  |  |  |  |  |
Soleil Terre Lune Phénomènes Les éclipses de LuneEn savoir plus: Une des démonstrations d'Aristarque |
En savoir plusLa démonstration suivante est issue de la traduction du Comte de Fortia d'Urban et se trouve dans la proposition VIII du Traité d'Aristarque. Pour rendre la démonstration plus lisible je l'ai retranscrite en termes mathématiques plus contemporains.
La proposition VIII est la suivante : La distance à laquelle le soleil se trouve de la terre est plus grande dix-huit fois, mais moindre vingt fois que celle à laquelle la lune se trouve de la terre.
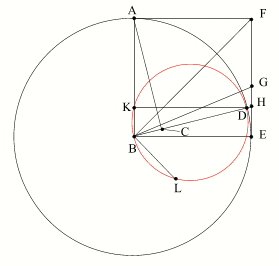
Soit A le centre du Soleil, B le centre de la Terre et C le centre de la Lune. Traçons le cercle (c) de centre B et de rayon AB, le rayon BD passant par C et faisant un angle de 3° avec le rayon BE perpendiculaire à BA (l'angle CBE est la trentième partie de l'angle droit). On construit le carré ABEF, ainsi que sa diagonale BF. Soit BG la bissectrice de l'angle EBF.
L'angle CBE est la trentième partie d'un angle droit (90°/30) et l'angle GBE est le quart d'un angle droit (90°/4), donc l'angle GBE vaut les 15/2 de l'angle CBE. Le rapport de EG sur EH est plus grand que le rapport des deux angles GBE et CBE, donc plus grand que 15/2.
BF est la diagonale du carré ABEF, donc le carré de BF est le double du carré de BE. De plus le carré construit sur FG est aussi le double du carré construit sur EG.
Or comme 49 est inférieur au double de 25, le carré de FG/EG = 2 est supérieur à 49/25, le rapport FG/EG est donc supérieur à 7/5.
Donc EF/EG = (EG+GF)/EG = 1 + GF/EG est supérieur à 12/5 ou 36/15.
Ainsi EG/EH est plus grand que 15/2 et EF/EG est supérieur à 36/15, donc EF/EH est supérieur à 18. Or EF = BE, donc BE/EH est supérieur à 18, et comme BH est supérieur à BE, BH/EH est également supérieur à 18. Or les triangles ABC et EBH sont semblables, donc les rapports BH/EH et AB/BC sont égaux et l'on a bien BA supérieur à 18 BC.
La distance Terre-Soleil est supérieure à 18 fois la distance Lune-Soleil.
Reste à prouver que ce rapport est inférieur à 20. Pour cela traçons la parallèle à BE, cette parallèle coupe AB en K. Traçons le cercle passant par les points BDK et soit L le point du cercle tel que LB soit le côté d'un hexagone inscrit dans ce cercle.
L'angle DBK est égal à l'angle DBE égal à la trentième partie d'un angle droit, l'arc de cercle BK vaut le double donc la quinzième partie d'un angle droit ou encore la soixantième partie de la circonférence.
Or BL est la sixième partie de cette même circonférence; donc l'arc BL est dix fois plus grand que l'arc BK. Or le rapport des cordes BL/BK est inférieur au rapport des arcs BL/BK, donc la corde BL est inférieure à dix fois la corde BK.
Or BD est égal à deux BL, donc BD est inférieur à 20 BK. Or les triangles DKB et ABC sont semblables donc BD/BK = AB/BC, donc AB est bien inférieur à 20 BC.
RemarqueBien évidemment, si l'on connaît la trigonométrie, cette longue démonstration élégante est remplacée par une simple équation à savoir : AB/BC = 1/sin 3° d'où AB/BC = 19,10.
 |  |