En savoir plus
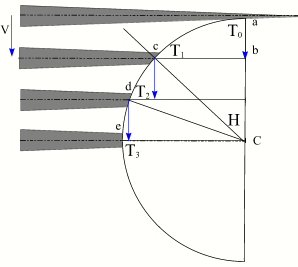
En réalité, le calcul de la vitesse de l'ombre à surface du sol est plus complexe, dans l'explication précédente nous avons fait des simplifications qui ne sont vraies que lorsque les vecteurs vitesses de l'ombre et du sol sont colinéaires. Dans un premier temps, on peut supposer une Terre fixe avec une ombre de la Lune se déplaçant avec une vitesse constante V par rapport à la Terre. Sur la figure ci-contre nous avons tracé la position du cône d'ombre et de son axe à des instants T0, T1, T2 et T3 séparés par un intervalle de temps dt constant. Durant le premier intervalle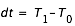 
l'ombre de la Lune s'est déplacée de 
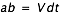dans l'espace et dans le plan passant par le centre de la Terre et normal à l'axe du cône d'ombre (plan de Bessel), alors que l'ombre a parcouru l'arc ac à la surface de la Terre, à la fin de l'intervalle dt suivant l'ombre se trouve en d et a parcouru l'arc cd, puis à la fin de l'intervalle dt suivant elle se trouve en e ayant parcouru l'arc de. Nous avons donc la projection d'un mouvement rectiligne uniforme sur un cercle de la sphère terrestre. Dans l'hypothèse d'une Terre fixe, ce cercle est l'intersection de la droite Soleil-Lune avec la sphère terrestre. La vitesse de l'ombre à la surface de la Terre est donnée par la formule dl/dt = V/sin(H), comme on le voit elle est très grande, proche de a (H~0°) et égale à V en e (H=90°). La vitesse de la projection de l'ombre est donc très grande après le premier et avant le dernier contact avec la surface terrestre (l'axe est tangent à la sphère terrestre).
Soleil Terre Lune Phénomènes
