En savoir plus: Le calcul des rayons de l'ombre et de la pénombre

En savoir plus

Soit P un plan normal à l'axe des cônes d'ombre et de pénombre, ρ et σ les rayons des cercles définis par les intersections du cône de d'ombre et du cône de pénombre avec ce plan. Soit R_s le rayon solaire, R_m le rayon lunaire, r_s et r_m les distances respectives du centre du Soleil et du centre de la Lune au plan P. Une simple application du théorème de Thalès nous donne les valeurs de ρ et σ en fonction de R_s, R_m, r_s et r_m.

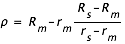
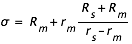
Lorsque l'éclipse est annulaire le plan P coupe l'axe des cônes après le sommet du cône d'ombre, il coupe donc le prolongement du cône d'ombre. Les formules précédentes sont également applicables si l'on accepte que les rayons aient des valeurs négatives.