Lever et coucher d'un astre en un lieu donné

Lever et coucher des astres

Pour calculer l'instant du lever ou du coucher d'un astre dont on suppose connues les coordonnées équatoriales approchées α et δ au moment du phénomène considéré, on calcule d'abord l'angle horaire H au moment du lever ou du coucher par la formule :

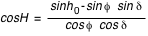cosH=(sinh_0-sin*phi*sin*delta)/(cos*phi*cos*delta) où

φ est la latitude du lieu et h₀ un angle petit qui sera défini plus loin. Le temps sidéral approché du lever est alors :

(2a) 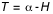T=alpha-H ;

et celui du coucher,

(2b) 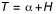T=alpha+H .

On calcule ensuite, à partir de T, l'instant du phénomène en temps universel comme on l'a expliqué dans les paragraphes précédents.

Si l'astre se déplace rapidement sur la sphère céleste (c'est le cas pour le Soleil, certaines planètes et surtout la Lune), on calcule pour l'instant trouvé des coordonnées α et δ plus exactes en interpolant les tables et l'on recalcule H puis T, par les formules (1) et (2), d'où l'instant du phénomène en UT. Pour la Lune, on est quelquefois amené à effectuer une itération supplémentaire.

Quant à h₀, son expression générale est la suivante :

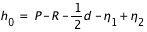h_0=P-R-(1/2)*d-eta_1+eta_2 ,

P est la parallaxe. On la néglige pour tous les astres sauf pour la Lune pour laquelle P = 57'.

R est la réfraction à l'horizon. Les tables du présent volume utilisent la théorie de la réfraction de Radau qui conduit à R = 36'36", mais l'on pourra utiliser la valeur R = 34' adoptée dans les Ephémérides Nautiques publiées par le Bureau des longitudes et dans d'autres publications étrangères.

(1/2) d est le demi-diamètre apparent de l'astre. On l'introduit dans la formule quand on calcule le lever et le coucher du bord supérieur du Soleil et de la Lune et non pas le lever et le coucher du centre de l'astre. On prend, aussi bien pour le Soleil que pour la Lune, (1/2) d = 16'.

Si l'observateur est à une altitude A au-dessus du niveau de la mer, on introduit dans 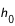h_0 l'angle 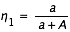eta_1=a/(a+A) , où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :

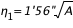eta_1=1'56"*racine(A) ,

A étant exprimé en mètres.

Si l'on cherche le lever ou le coucher d'un astre en un lieu dont l'horizon est limité par des collines ou des montagnes d'altitude 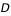situées à la distance 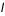de l'observateur, on ajoutera à 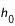h_0 l'angle 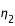eta_2 tel que :

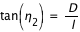tan(eta_2)=D/l .

On ne cherchera pas à obtenir les instants du lever ou du coucher des astres avec une précision supérieure à une minute, la valeur exacte de la réfraction à l'horizon au moment du phénomène étant trop mal connue.