
Exercice |
Difficulté : ☆☆ Temps : 30 min
Avant de regarder l’expansion dans notre univers, illustrons ce phénomène dans un univers à deux dimensions et sphérique. Imaginons que nous vivons à la surface d'une sphère de rayon 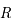 . Cet univers a pour caractéristique d’être de taille finie, avec une surface égale à
. Cet univers a pour caractéristique d’être de taille finie, avec une surface égale à 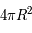 , mais sans bord. De fait, il est possible d’aller indéfiniment en ligne droite sans jamais trouver d’obstacle. Imaginons que cet univers est en expansion, le rayon
, mais sans bord. De fait, il est possible d’aller indéfiniment en ligne droite sans jamais trouver d’obstacle. Imaginons que cet univers est en expansion, le rayon 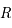 évoluant suivant la loi
évoluant suivant la loi 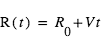 ,
,  en milliards d’années,
en milliards d’années, 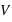 exprimant la vitesse d'expansion qui vaut 1000 Mpc par milliard d'années, et
exprimant la vitesse d'expansion qui vaut 1000 Mpc par milliard d'années, et 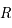 en Mpc, avec
en Mpc, avec 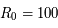 Mpc.
Mpc.
Quelle est la surface de cet univers à 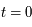 ?
?
Soit deux points proches supposés sans interaction. A 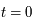 , leur distance, à la surface de la sphère, est notée
, leur distance, à la surface de la sphère, est notée 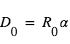 , avec
, avec 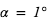 . Au fil du temps, cette distance va s’accroître. Quelle est leur distance en Mpc au temps
. Au fil du temps, cette distance va s’accroître. Quelle est leur distance en Mpc au temps 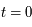 et quelle est sa loi d'évolution ?
et quelle est sa loi d'évolution ?
Combien vaudront le rayon et la surface de cet univers à 10 milliards d'années ?
Donner la vitesse à laquelle les deux points s'éloignent l'un de l'autre en fonction de la distance initiale.