
|
Difficulté : ☆☆☆ Temps : 45 min
Le spectromètre HARPS, mis en service au printemps 2003 à La Silla, l'un des sites chiliens de l'ESO, a pour but la recherche des exoplanètes. On se propose ici de retrouver quelques-unes des qualités qui lui permettent d'atteindre les objectifs scientifiques fixés.
Le spectromètre est installé derrière le télescope de 3.6 m de l'ESO. Sa pièce principale, le réseau, présente une hauteur 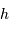 de 20 cm. Déterminer le grossissement
de 20 cm. Déterminer le grossissement 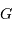 du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
Montrer qu'une déviation 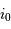 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 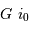 de l'angle dispersé.
de l'angle dispersé.
Rappeler l'expression donnant les variations 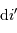 de l'angle de dispersion
de l'angle de dispersion 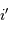 en fonction des variations de longueur d'onde
en fonction des variations de longueur d'onde 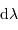 , du pas
, du pas 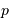 du réseau, et selon l'ordre d'interférence
du réseau, et selon l'ordre d'interférence 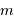 .
.
On cherche à déterminer le champ objet maximal, qui permette
d'atteindre un pouvoir de résolution 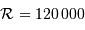 . Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
. Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
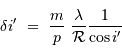
et conclure. On fera l'application numérique avec les données :
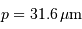 ,
, 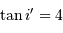 et un ordre d'interférence
et un ordre d'interférence 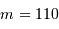 à
à 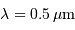 :
: