Apprendre

Objectifs

Décrire l'allure de l'interférogramme.

Le spectre théorique initial

Le spectre comprend les données en entrée :

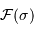L'intensité spectrale $\mathcal{F} (\sigma)$ .
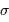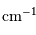L'unité spectrale employée est le nombre d'onde, $\sigma$ , exprimé en ${\,\mathrm{cm}}^{-1}$ .

L'avantage de travailler avec une telle unité spectrale est d'avoir des variables directement conjuguées entre le spectre et l'interférogramme :

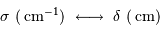
$\sigma \ ( {\,\mathrm{cm}}^{-1}) \ \longleftrightarrow \ \delta\ ( {\,\mathrm{cm}})$

Ces unités employées, quoique hors SI, présentent l'avantage d'être inverses l'une de l'autre.

Interférogramme et TF

L'interférogramme calculé représente la quantité :

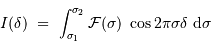
$I(\delta) \ = \ \int_{\sigma_1}^{\sigma_2} \mathcal{F} (\sigma) \ \cos 2\pi \sigma \delta \ {\mathrm{d}} \sigma$

où l'on reconnaît la partie réelle de la TF de la densité spectrale 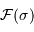$\mathcal{F} (\sigma)$ .

L'interférogramme réalise physiquement la TF de la distribution spectrale de la source. La TF inverse de l'interférogramme, calculée, permet de remonter au spectre.

Etendue de faisceau

L'interféromètre étant réglé en anneaux, le principe instrumental ne nécessite pas l'introduction d'une fente d'entrée, contrairement à un spectromètre à réseau. L'étendue de faisceau n'est donc pas drastiquement limitée par une fente ; en pratique, elle est limitée par la nécessité de travailler dans un coeur de frange.

Ceci est convenablement dimensionné dans un exercice.