
 Interférogramme d'un doublet
Interférogramme d'un doublet
Difficulté : ☆☆
Temps : 30 min
On illumine un interféromètre de Fourier avec une source ponctuelle présentant un doublet, aux nombres d'onde 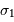 et
et 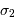 voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
Question 1)
Déterminer l'expression de l'interférogramme 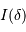 . Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
. Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
AideAideSolution
Les 2 ondes peuvent-elles être cohérentes ?
On rappelle :
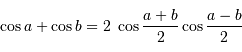
Les 2 ondes monochromatiques sont incohérentes entre elles.
Le signal d'interférence s'écrit donc, pour les raies supposées monochromatiques, comme somme des intensités :
![I(\delta) \ = \ I_0 \ \left[1 + \cos(2\pi \sigma_1 \delta)\right] + I_0 \ \left[1 + \cos(2\pi \sigma_2 \delta)\right]](../pages_fourier/equations_fts-interferogramme/equation14.png)
On en déduit :
![I(\delta) \ = \ 2\ I_0 \ \left[1 +\cos\bigl(\pi (\sigma_1+\sigma_2) \delta\bigr) \cos\bigl(\pi (\sigma_1-\sigma_2) \delta\bigr)\right]](../pages_fourier/equations_fts-interferogramme/equation15.png)
On y reconnaît un terme d'interférence, de fréquence spatiale 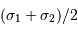 , modulé par une enveloppe de fréquence
, modulé par une enveloppe de fréquence 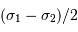 .
.
Question 2)
Déterminer la période des battements et représenter l'allure de l'interférogramme, pour le doublet du sodium :
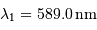 et
et 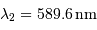 .
.
Solution
Les nombres d'ondes respectifs valent 16961 et 16978 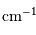 , soit une demi-différence de
, soit une demi-différence de 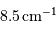 .
.
La fréquence spatiale des battements, d'après ce qui précède, vaut 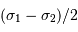 , la période spatiale est donc :
, la période spatiale est donc :
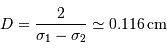
D'où l'allure de l'interférogramme :
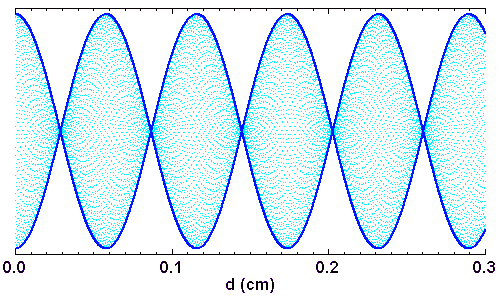
Les battements, de période 0.116 cm, sont seuls représentés, l'interférogramme ayant lui une période rapide de
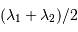
.
Crédit :
ASM

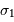 et
et 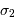 voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
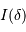 . Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
. Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
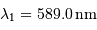 et
et 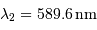 .
.