La relativité générale |
La relativité restreinte n'a cependant pas résolu tous les problèmes. Elle s'est montrée incapable d'incorporer la gravitation de manière satisfaisante et certaines expériences semblent toujours prouver qu'il existe un référentiel absolu. Par exemple, l'expérience du pendule de Foucault semble indiquer que l'on peut mesurer le mouvement de la Terre par rapport à un référentiel absolu. Où donc se trouve la contradiction ? Einstein va étendre pour cela la relativité restreinte à la gravitation. Pour cela Einstein va énoncer le principe d'équivalence. L'identité entre la masse gravifique et la masse inertielle devient un postulat de base de la théorie. Ainsi, il n'est pas possible, localement, de distinguer une force créée par une accélération d'une force créée par la gravitation. Cette identité a conduit Einstein à penser qu'un laboratoire en chute libre dans un champ gravitationnel constitue en quelque sorte l'extension naturelle du concept de système de référence inertiel de l'ancienne mécanique. On est ainsi amené à postuler que "tous les systèmes de référence en chute libre sont équivalents pour l'expression des lois physiques non gravitationnelles, quel que soit leur état de mouvement et leur localisation". Cet énoncé constitue ce qu'on appelle aujourd'hui le principe d'équivalence d'Einstein.
Il faut souligner à ce propos que ce principe n'édicte rien sur la description des phénomènes gravitationnels eux-mêmes. Ainsi, il ne postule pas que deux laboratoires en chute libre situés en des endroits différents vont trouver la même valeur pour la constante de la gravitation G (étant admis qu'ils sont munis d'horloges et de mètres de même fabrication). Autrement dit, le principe d'équivalence d'Einstein ne rejette pas a priori que la "vraie théorie relativiste de la gravitation" puisse prédire que G varie avec le temps et le lieu. Ce principe permet donc des généralisations de la relativité générale, généralisations dont les vérifications font l'objet de nombreuses recherches actuelles.
L'idée qu'en présence d'un champ gravitationnel, ce sont les référentiels en chute libre qui doivent remplacer les référentiels inertiels en amène très naturellement une autre : les référentiels en chute libre ne peuvent être que locaux, car un vrai champ de gravitation (celui de la Terre par exemple) n'est pas uniforme. En effet, la non uniformité entraîne qu'aucun mouvement global du système de référence ne peut supprimer partout le champ de la Terre. D'où l'idée que le principe d'équivalence d'Einstein, qui est purement local, n'interdit pas à la géométrie de l'espace-temps de changer d'un point à un autre. Au contraire, un tel changement de géométrie permet de résoudre le problème de la gravitation avec une extrême élégance conceptuelle. Le principe d'inertie galiléen nous dit qu'en l'absence de tout champ de force, un point matériel a un mouvement rectiligne uniforme dans tout référentiel galiléen. Or, une droite est une géodésique de l'espace euclidien. Il est dès lors naturel de considérer le mouvement d'une particule en chute libre dans un champ gravitationnel comme défini par une géodésique d'une métrique plus complexe qu'une métrique euclidienne. En fait, Einstein a introduit une généralisation dite "pseudo-riemanienne" de la métrique spatio-temporelle de la relativité restreinte.
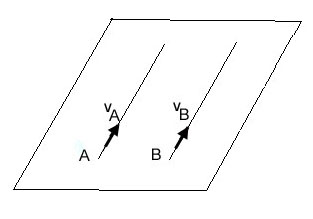
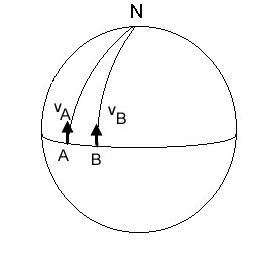
Nous donnons ci-dessous une analogie qui permet de comprendre pourquoi une métrique non euclidienne peut rendre compte de façon simple d'une force de gravitation.