La seconde classe d'indicateurs de distances est basée non plus sur les caractéristiques physiques d'un objet, mais sur les propriétés statistiques de familles d'objets galactiques ou sur les propriétés globales des galaxies elles-mêmes.
La seconde classe d'indicateurs de distances est basée non plus sur les caractéristiques physiques d'un objet, mais sur les propriétés statistiques de familles d'objets galactiques ou sur les propriétés globales des galaxies elles-mêmes.

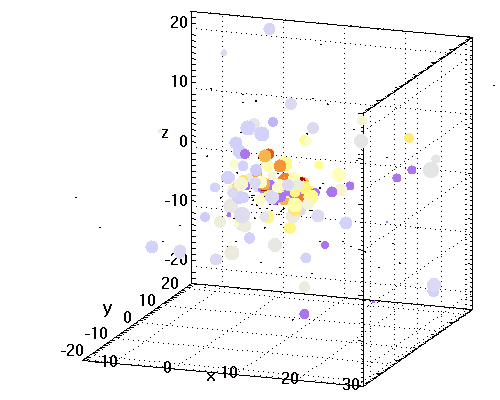
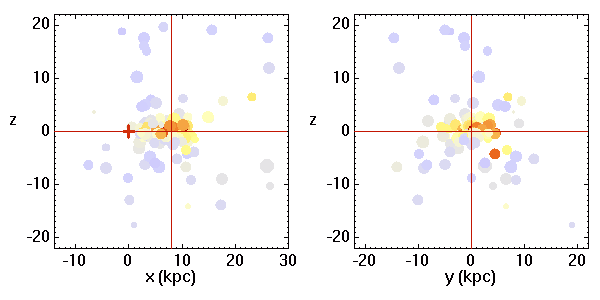
Les amas globulaires regroupent un grand nombre d'étoiles nées au sein d'un même nuage d'hydrogène. Ils sont majoritairement composés d'étoiles vieilles, et présentent une distribution à symétrie sphérique, contrairement aux amas ouverts.


La distribution des amas dans notre Galaxie présente la symétrie sphérique.
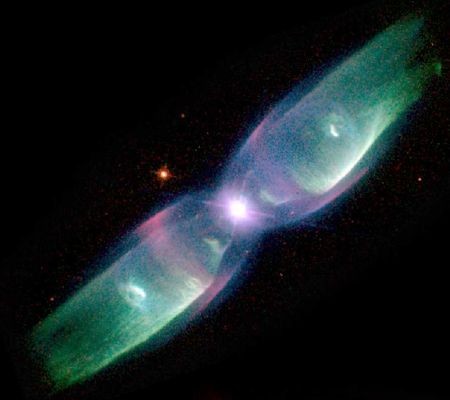
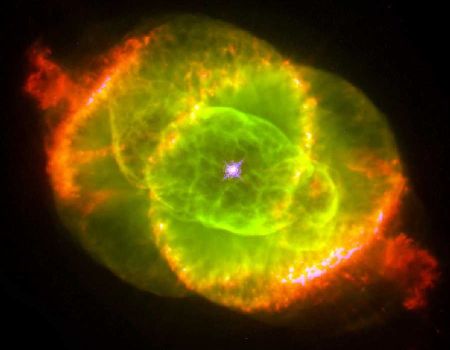
Les nébuleuses planétaires n'ont rien à voir avec une planète ... mis à part l'héritage de leur nom, lorsqu'elles apparaissaient semblables à un objet étendu de type planète. Mais il s'agit d'étoiles entourées de coquilles de gaz, matière éjectée par une étoile en fin de vie.
L'identification de propriétés statistiques permet de faire le lien entre une classe d'objets observée à faible ou grande distance. Ceci est bien sûr mis à profit pour la mesure de distance.
L'étude des amas globulaires dans le halo d'une galaxie dont on connaît la distance permet de construire la distribution de leurs luminosités. D'une galaxie à l'autre, on retrouve la même distribution, et cette uniformité est encore renforcée lorsque les galaxies hôtes ont des métallicités et des types morphologiques voisins.
De même, on observe pour les galaxies d'un même amas de galaxies que le pic de la distribution correspond à une même magnitude apparente. La position de ce maximum, calibrée dans notre galaxie au moyen de 100 amas globulaires correspond à une magnitude absolue de
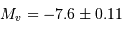 , pour un écart type
, pour un écart type 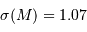 .
.
On peut ainsi en principe, en comparant la distribution des magnitudes apparentes des amas globulaires de différentes galaxies, obtenir des distances relatives. La réalité est bien sûr plus complexe, puisqu'il faut être capable d'estimer la métallicité moyenne de chaque galaxie, mesure difficile à réaliser car indissociable des effets de l'extinction ou du rougissement interstellaire. L'autre difficulté relève du fait qu'il faut pouvoir isoler chaque amas globulaire et corriger des éventuelles et probables superpositions d'étoiles extérieures, et aussi disposer de mesures photométriques suffisamment profondes pour que le maximum de la distribution de la fonction de luminosité des amas globulaires soit atteint.
Sur le même principe, la luminosité moyenne ou la taille moyenne des régions HII représente également un bon indicateur de distance. Ce sont des nuages de gaz très lumineux, ionisés par le rayonnement ultraviolet intense d'étoiles jeunes et très chaudes (de type spectral O ou B).
Les régions HII sont généralement observées dans les nuages moléculaires, sites privilégiés de la formation stellaire. Leur forme est à peu près sphérique si le milieu est homogène, et leur extension spatiale relativement uniforme, de l'ordre de 200 pc.
Enfin, on peut considérer la fonction de luminosité des nébuleuses planétaires D'après la théorie de l'évolution stellaire, elle possède une limite supérieure universelle, indépendante du type morphologique, de la métallicité, de l'âge, ou de la taille de la galaxie hôte.
Les nébuleuses planétaires sont des enveloppes gazeuses qui entourent une étoile chaude. Elles forment une coquille en expansion autour du résidu de l'étoile qui se contracte pour former une naine blanche. Repérer les nébuleuses planétaires les plus brillantes d'une galaxie permet donc estimer sa distance. Cette méthode souffre cependant de quelques biais systématiques : les étoiles les plus massives évoluant très rapidement, il est rare de pouvoir observer une nébuleuse planétaire vraiment très lumineuse. A cela s'ajoute un effet de population : on a plus de chance d'observer une nébuleuse planétaire très lumineuse dans une galaxie géante qui compte de nombreuses étoiles, que dans une galaxie naine. Les galaxies géantes apparaîtraient donc plus proches que les petites...
Localisation des régions HII dans une paire de galaxies en collision et comparaison avec une nébuleuse à émission, une région HII de notre propre Galaxie : la grande nébuleuse d'Orion.


E. Hubble proposa en 1926 une classification des galaxies selon trois grandes catégories : elliptiques (E), spirales (barrées SB ou non S) et irrégulières. On y distingue des sous-classes selon le degré d'ellipticité ou le développement des bras spiraux des galaxies.
Les galaxies elliptiques ont l'aspect de sphéroïdes plus ou moins aplatis. Elles contiennent une population d'étoiles plutôt vieilles et très peu de gaz ou de poussières. Les galaxies les plus massives sont des galaxies elliptiques, mais il existe aussi une classe de galaxies elliptiques naines, en général satellites de galaxies plus grosses.
Les galaxies spirales sont disposées en deux séquences parallèles. Elles contiennent une grande quantité de gaz et de poussières, concentrée dans leur disque, en particulier le long des bras spiraux. On y distingue plusieurs populations d'étoiles d'âges différents, les plus vieilles étant concentrées dans le bulbe central et dans le halo, les plus jeunes étant réparties dans le disque. Les galaxies spirales sont caractérisées morphologiquement par l'importance relative du bulbe, qui décroît du type Sa (ou SBa) vers le type Sc (ou SBc), et le degré d'enroulement des bras autour du noyau. Les bras sont très serrés pour les Sa (ou SBa) et s'ouvrent progressivement jusqu'aux Sc (ou SBc).
Dans les galaxies spirales barrées, le noyau est traversé par une barre d'étoiles, aux extrémités de laquelle débutent les bras spiraux. La présence de gaz et de poussières, de régions ionisées et d'étoiles jeunes s'accroît régulièrement vers les Sc (ou SBc).
Les galaxies irrégulières ont, comme leur nom l'indique, une forme mal définie.
A la classification de Hubble s'est rajoutée la classe des lenticulaires ou S0. Ce sont des galaxies à très gros bulbe central possédant aussi un disque aplati d'étoiles. Ce disque ne contient pas de bras spiraux, et en général pas ou peu de gaz et de poussières.
Enfin, il existe une dernière catégorie, découverte récemment et qui pourrait représenter en nombre presque 50% de la population totale des galaxies, c'est la classe des naines irrégulières. Ce sont des objets à faible brillance de surface, donc difficiles à détecter en optique, mais qui comptent pourtant parfois presque autant d'hydrogène atomique que certaines spirales géantes.
La relation de Tully-Fisher relie la magnitude absolue d'une galaxie à sa vitesse de maximale de rotation.
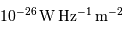 ), fonction de la vitesse de rotation mesurée par effet Doppler.
), fonction de la vitesse de rotation mesurée par effet Doppler.
La relation de Tully-Fisher, du nom des deux astronomes anglais qui l'ont découverte en 1977, relie la vitesse maximale 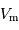 de rotation d'une galaxie spirale à sa luminosité. Cette loi empirique prend la forme suivante :
de rotation d'une galaxie spirale à sa luminosité. Cette loi empirique prend la forme suivante :
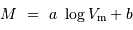
où les coefficients 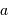 et
et 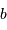 représentent la pente et le point-zéro de la relation. Pour la bande photométrique B, les valeurs acceptées actuellement sont :
représentent la pente et le point-zéro de la relation. Pour la bande photométrique B, les valeurs acceptées actuellement sont :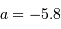 et
et 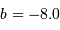 .
.
La mesure du maximum de la vitesse de rotation observée permet alors d'estimer la magnitude absolue, et par comparaison avec l'éclat apparent mesuré, d'en déduire la distance. C'est une relation de type masse-luminosité qui rend compte du fait que, plus une galaxie est massive :
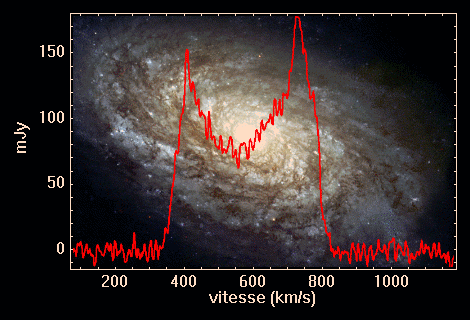
La vitesse de rotation est mesurée à partir de l'émission du gaz contenu dans le disque. Cette mesure se fait essentiellement soit à partir d'une courbe de rotation de la galaxie obtenue en spectroscopie optique (analyse de la raie 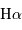 de l'hydrogène en émission), soit à partir du spectre radio
autour de 1420 MHz (analyse de la raie à 21 cm de l'hydrogène neutre). Ce critère permet d'atteindre une précision de 15 à 25 % sur les distances.
de l'hydrogène en émission), soit à partir du spectre radio
autour de 1420 MHz (analyse de la raie à 21 cm de l'hydrogène neutre). Ce critère permet d'atteindre une précision de 15 à 25 % sur les distances.
On obtient un bon étalonnage de la relation Tully-Fisher en utilisant les étoiles céphéides qui ont été observées par le télescope spatial Hubble dans une bonne trentaine de galaxies spirales proches.
La méthode des galaxies sosies suppose que deux galaxies ayant le même type morphologique et la même vitesse de rotation ont aussi en moyenne la même luminosité. Il suffit alors de comparer l'éclat observé à l'éclat d'un étalon de distance connue pour avoir la distance de la galaxie. Il n'est pas nécessaire alors de mesurer la pente de la relation. Il existe aujourd'hui des mesures de vitesse de rotation pour environ 16600 galaxies de notre univers proche.
La relation Faber-Jackson peut comme la précédente être assimilée à un relation masse-luminosité. Elle relie la luminosité intrinsèque d'une galaxie elliptique ou lenticulaire (mais aussi du bulbe d'une spirale) à la dispersion des vitesses des étoiles mesurées en son coeur. Cette dispersion centrale des vitesses est mesurée à partir de l'élargissement de certaines raies d'absorption dans le spectre optique des galaxies. Ces mesures sont très délicates car il faut pouvoir séparer l'élargissement provenant des mouvements des étoiles dans la galaxie, de l'élargissement provoqué par la rotation ou les turbulences dans les enveloppes des étoiles elles-mêmes. La relation possède une dispersion relativement importante d'environ 0.6 magnitude, qui se traduit par une incertitude d'environ 30 % sur les distances estimées. Ce type de mesure est disponible pour environ 4000 galaxies.
L'appliquette ci-jointe décrit la morphologie d'une galaxie spirale.

A l'aide de l'appliquette ci-dessous, on se propose d'étalonner la relation de Tully-Fisher.

La solution :
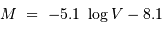
Difficulté : ☆ Temps : 20 min
| PGC | 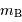 |  (deg) (deg) |
| 49157 | 13.03 | 66.6 |
| 49322 | 15.20 | 67.8 |
| 49275 | 13.34 | 64.1 |
| 48925 | 15.23 | 82.3 |
PGC49157 
PGC49322 
PGC49275 
PGC48925 
Mesurer la largeur de la raie à 21 cm des galaxies PGC 48925, PGC 49157, PGC 49322 et PGC 49275 à partir des spectres disponibles.
La mesure se fait habituellement à 20% de la hauteur de la raie, par rapport à une ligne horizontale passant au milieu du bruit de fond.
Les largeurs de raies sont perturbées par la turbulence  .
En déduire les valeurs
.
En déduire les valeurs 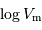 en prenant en compte l'effet de projection et la composante de turbulence de qui élargit la raie. Comparer aux données de la base.
en prenant en compte l'effet de projection et la composante de turbulence de qui élargit la raie. Comparer aux données de la base.
Difficulté : ☆☆ Temps : 45 min
Cet exercice repose sur la consultation de divers documents issus de l'interrogation de la base de données extragalactiques LEDA qui contient les données de près de 3 millions de galaxies. L'exploration est faite dans une région du ciel au voisinage de la galaxie spirale PGC 49347 (NGC5350) pour montrer un exemple de recherche de groupement physique de galaxies et un exemple d'application de la relation de Tully-Fisher à un amas. Les galaxies sont repérées par un numéro PGC (principal galaxy catalog). Les paramètres sont les suivants :
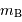 .
.On dispose d'un tableau des objets répertoriés, classés par ascension droite croissante, et de quatre "zooms" centrés sur quelques galaxies ou groupes intéressants. Dans le tableau, l'inclinaison est donnée en degré, la vitesse radiale en km/s.



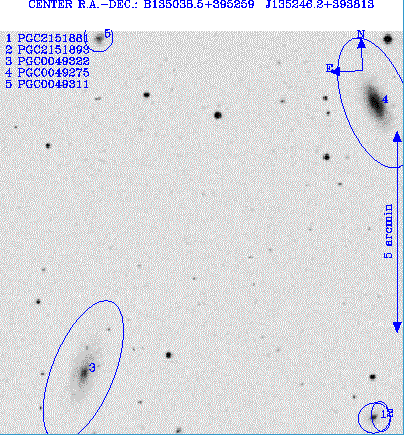
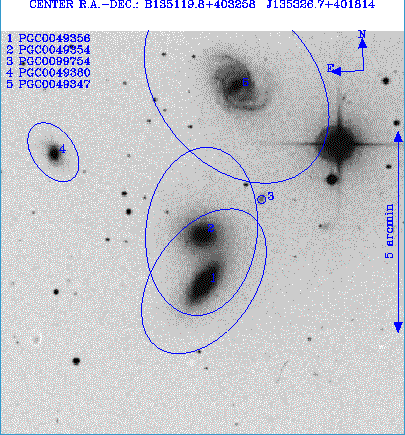


A l'aide des appliquettes, identifier les principales galaxies. Repérer les différents types morphologiques représentés et les comparer à la table. Identifier la signification des paramètres angulaires pa et i de la table.
Vérifier que PGC 49354 est presque vue de face, et que PGC 49389 est quasiment vue par la tranche.
Peut-on dire que PGC 49356 et PGC 49389 forment une paire de galaxies ?
Comment identifier à partir des divers documents les galaxies formant un petit groupe avec PGC 49347 ?
Rechercher les groupements physiques de galaxies présents dans le champ. Y a-t-il des galaxies qui sont proches sans être associées ?
Difficulté : ☆ Temps : 45 min
Cet exercice est basé sur le résultat de l'exercice analysant un champ galactique, c'est à dire de la liste des membres de l'amas principal du champ extragalactique extrait de la base LEDA et centré sur la galaxie PGC 49347 (NGC 5350). Dans le tableau, l'inclinaison est donnée en degré, la vitesse radiale en km/s.


Expliciter les critères qualitatifs définissant les galaxies utilisables pour appliquer la relation de Tully-Fisher. Peut-on utiliser des galaxies vues quasiment de face ?
Quantitativement, on fixe pour les critères précédents, une
vitesse radiale dans l'intervalle 2000 - 2600 km/s, une inclinaison
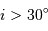 . Sélectionner les galaxies en conséquence.
. Sélectionner les galaxies en conséquence.
Calculer pour chaque galaxie sa magnitude apparente bleue 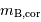 corrigée des effets d'extinction. Le tableau représente les corrections galactique et intergalactique.
Représenter les points
corrigée des effets d'extinction. Le tableau représente les corrections galactique et intergalactique.
Représenter les points 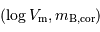 (logvrot, mbc)sur un graphe et évaluer la pente de l'estimation linéaire observée
(logvrot, mbc)sur un graphe et évaluer la pente de l'estimation linéaire observée 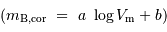 .
.
Dans le tableau, l'inclinaison est donnée en degré, la vitesse radiale (vrad) en km/s, et la vitesse de rotation (logvrot 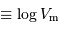 ) en échelle logarithmique, avec également comme unité de vitesse le km/s.
) en échelle logarithmique, avec également comme unité de vitesse le km/s.
Calculer l'ordonnée à l'origine 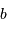 en forçant une pente de -5.8, d'après la pente théorique.
en forçant une pente de -5.8, d'après la pente théorique.
Calculer la distance de l'amas en utilisant la relation calibrée en magnitude
absolue : 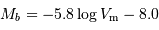
Estimer la vitesse radiale moyenne 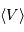 de l'amas et en déduire une valeur de la constante de Hubble
de l'amas et en déduire une valeur de la constante de Hubble 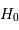 (constante d'expansion).
(constante d'expansion).
Difficulté : ☆ Temps : 25 min
Un exercice précédent a permis de repérer les galaxies du groupe de PGC 49347 (NGC 5350).
A l'aide des valeurs tabulées dans les 2 appliquettes de ce précédent exercice, identifier dans les galaxies du groupe de PGC 49347 une galaxie sosie de M31 (galaxie Sb, d'inclinaison 77 deg, de vitesse maximale de rotation 250 km/s), présentant un triplet de paramètres le plus voisin possible. Calculer son module de distance en fonction de celui de M31.
[2 points]
Calculer la distance de cette galaxie sosie, sachant que la magnitude apparente de M31 vaut 3.20 et son module de distance 24.6. En déduire une valeur du taux d'expansion 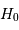 .
.
[2 points]
L'expansion de l'Univers a été décelée par l'examen de raies galactiques sur des objets de plus en plus lointains.
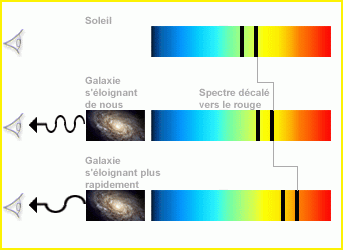

Ce décalage varie en fonction de la distance, selon la loi de Hubble.
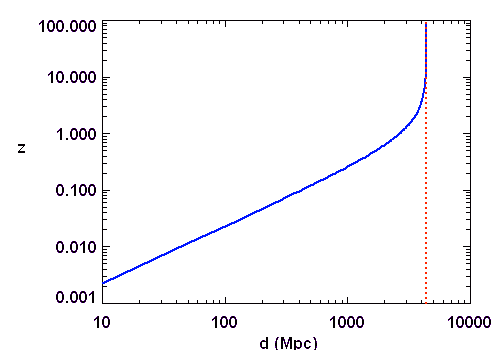
Un projet d'envergure a cartographié les galaxies, en déduisant leur distance de leur éloignement Doppler.
Le plus utilisé des estimateurs de distance reste certainement la loi de Hubble. En 1929, analysant les raies dans les spectres des galaxies, Edwin Hubble montre que les spectres apparaissent systématiquement décalés vers le rouge. Ce décalage spectral, interprété via l'effet Doppler dû à la vitesse de fuite des galaxies, est proportionnel à la distance des galaxies.
Plus une galaxie est éloignée, plus vite elle s'éloigne. Cela signifie que l'Univers est en expansion.
Ce concept d'un univers évolutif, en expansion, est contenu dans les équations de la relativité générale. La relativité générale explique que ce ne sont pas les galaxies qui se déplacent dans l'espace, mais le tissu spatial lui-même qui se dilate.
Les mesures actuelles de la constante de proportionnalité 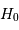 (ou constante de Hubble) donnent une valeur comprise entre 50 et 70 km/s/Mpc.
(ou constante de Hubble) donnent une valeur comprise entre 50 et 70 km/s/Mpc.
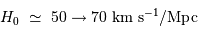
La valeur mesurée par le satellite Planck est de 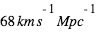
La proportionnalité entre vitesse et distance n'est cependant valable qu'aux petites échelles (inférieures à 5 milliards d'années de lumière), où les effets de la courbure de l'espace ne se font pas sentir.
Inversement, les mouvements particuliers des galaxies étant de l'ordre de quelques centaines de km/s, la vitesse radiale observée n'est un bon indicateur de la vitesse cosmologique qu'au-delà d'une certaine distance, quand ces mouvements deviennent négligeables devant l'expansion (au-delà d'une centaine de millions d'années de lumière). Ce sont donc les redshifts, même s'ils donnent une mesure de distance quelque peu "floue" à cause des mouvements locaux, qui ont permis les premières cartographies 3D de notre univers proche et la découverte des grandes structures : amas, filaments, bulles et grands murs que l'on observe jusqu'à des échelles de quelques centaines de millions d'années de lumière.
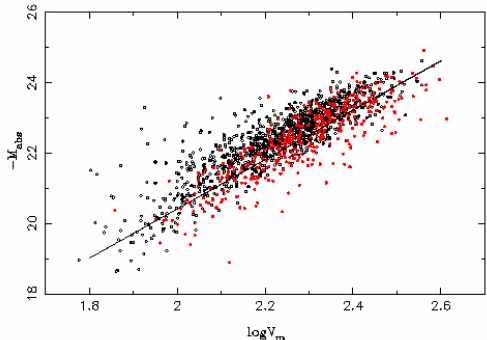
Les observations extragalactiques portent sur des objets certes intrinsèquement très lumineux, mais apparemment très peu lumineux, et souvent si peu lumineux que la non détection des moins lumineux d'entre eux peut provoquer un biais dans les résultats observationnels. Ce biais peut affecter toute mesure statistique supposant, à tort, une population homogène d'objets.
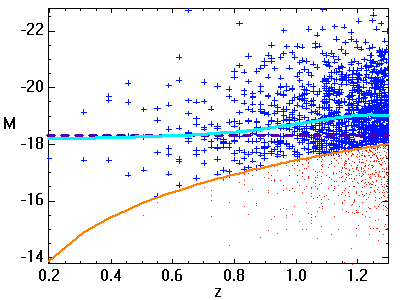
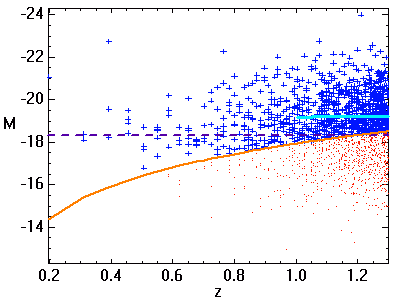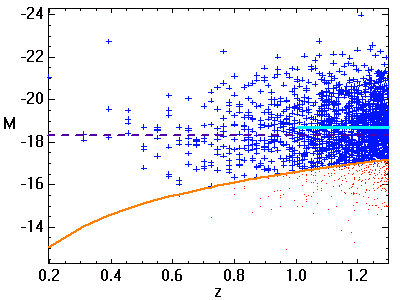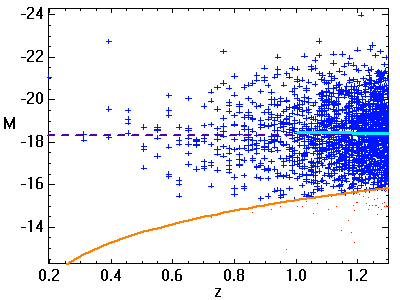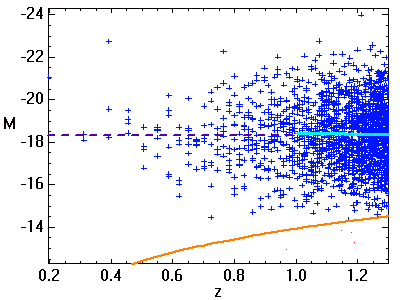
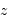 . Le nombre d'objets observés croît comme le carré de la distance. A grande distance, la non-détection des moins lumineux (objets indiqués en rouge) biaise la distribution observée. La moyenne des magnitudes absolues (en bleu) s'en ressent : elle est inférieure à ce que l'on observerait sans biais.
. Le nombre d'objets observés croît comme le carré de la distance. A grande distance, la non-détection des moins lumineux (objets indiqués en rouge) biaise la distribution observée. La moyenne des magnitudes absolues (en bleu) s'en ressent : elle est inférieure à ce que l'on observerait sans biais.
Les premiers travaux utilisant la relation Tully-Fisher conduisirent dans les années 1980 à une valeur élevée de la constante de Hubble - de l'ordre de 100 km/s/Mpc - ainsi qu'à une croissance de 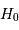 avec la distance. Ces résultats proviennent de la nature statistique de la relation
Tully-Fisher et du fait que les échantillons sont toujours limités en magnitude apparente.
avec la distance. Ces résultats proviennent de la nature statistique de la relation
Tully-Fisher et du fait que les échantillons sont toujours limités en magnitude apparente.
A toutes les galaxies ayant la même vitesse de rotation 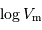 (ou appartenant à une classe de sosies), on attribue la même magnitude absolue (ou luminosité) selon la relation linéaire :
(ou appartenant à une classe de sosies), on attribue la même magnitude absolue (ou luminosité) selon la relation linéaire :
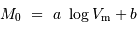
Chaque détermination individuelle souffre en fait d'une imprécision due à l'écart entre la magnitude
absolue exacte et la valeur moyenne 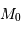 adoptée. Si on considère maintenant un grand nombre
d'objets, on détermine donc un ensemble de distances dont chacune est affectée d'une erreur, les unes étant surestimées, les autres sous-estimées. On espère cependant qu'elles soient exactes en moyenne.
adoptée. Si on considère maintenant un grand nombre
d'objets, on détermine donc un ensemble de distances dont chacune est affectée d'une erreur, les unes étant surestimées, les autres sous-estimées. On espère cependant qu'elles soient exactes en moyenne.
K.G. Malmquist (1920) a montré que ce n'est pas le cas si l'échantillon utilisé est limité en magnitude apparente : l'échantillon contient alors en effet une plus grande proportion de galaxies intrinsèquement plus lumineuses que 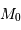 ,
et une moins grande proportion de galaxies moins lumineuses. La magnitude absolue moyenne de l'ensemble des galaxies du catalogue n'est donc pas égale, mais inférieure à
,
et une moins grande proportion de galaxies moins lumineuses. La magnitude absolue moyenne de l'ensemble des galaxies du catalogue n'est donc pas égale, mais inférieure à 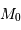 .
.
Il s'ensuit qu'en sous-estimant ainsi la luminosité moyenne des galaxies observées, on sous-estime leurs distances, et l'on surestime la constante de Hubble.
Si on suppose que les galaxies sont réparties uniformément dans l'espace, l'erreur statistique sur la magnitude absolue 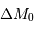 et donc sur le module de distance des galaxies peut s'exprimer de manière simple en fonction de la dispersion
et donc sur le module de distance des galaxies peut s'exprimer de manière simple en fonction de la dispersion 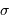 du critère de distance (l'incertitude moyenne par rapport à
du critère de distance (l'incertitude moyenne par rapport à 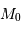 ) :
) :

Pour une dispersion 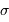 de l'ordre de 0.6 magnitude, typiquement ce que l'on obtient par la
relation Tully-Fisher
ou la méthode des sosies, cela donne sur le module de distance une erreur de - 0.5 magnitude. On obtient finalement sur la distance une sous-estimation de l'ordre de 23%, et une valeur de
de l'ordre de 0.6 magnitude, typiquement ce que l'on obtient par la
relation Tully-Fisher
ou la méthode des sosies, cela donne sur le module de distance une erreur de - 0.5 magnitude. On obtient finalement sur la distance une sous-estimation de l'ordre de 23%, et une valeur de 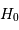 surestimée d'autant.
surestimée d'autant.
L'animation ci-jointe montre comment le biais de Malmquist dépend de la magnitude limite d'observation. Plus elle est élevée, moins le biais est important.
Difficulté : ☆☆☆ Temps : 1 h
On se propose d'estimer la constante de Hubble et l'âge de l'univers en utilisant les sosies d'une galaxie bien connue : la galaxie d'Andromède (M31). Le tableau donne les paramètres d'une trentaine de galaxies sélectionnées dans la base de données extragalactiques LEDA selon les critères de morphologie (spirale), d'inclinaison ou de rapport d'axe 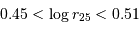 (
(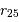 est le rapport du grand au petit axe, repéré à l'isophote de magnitude 25), vitesse de rotation (en km/s) dont le logarithme vérifie
est le rapport du grand au petit axe, repéré à l'isophote de magnitude 25), vitesse de rotation (en km/s) dont le logarithme vérifie 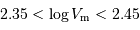 , et avec un seuil en magnitude
, et avec un seuil en magnitude 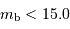 .
.
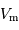 est le maximum de la vitesse de rotation dans le disque, et
est le maximum de la vitesse de rotation dans le disque, et 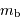 est la magnitude apparente dans la bande
est la magnitude apparente dans la bande 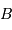 .
.
La magnitude apparente de M31 (PGC 2557) vaut 3.20 ; sa distance, déterminée au moyen de céphéides observées par le télescope spatial Hubble, est estimée à 0.841 Mpc, ce qui représente un module de distance de 24.6 (avec la distance exprimée en Mpc, 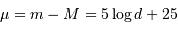 ).
Le tableau fournit, pour chaque galaxie repérée par son numéro PGC : la magnitude apparente mb, une valeur corrigée
).
Le tableau fournit, pour chaque galaxie repérée par son numéro PGC : la magnitude apparente mb, une valeur corrigée 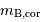 , le logarithme de la vitesse maximale de rotation de la galaxie (logv), et sa vitesse radiale héliocentrique (vrad).
, le logarithme de la vitesse maximale de rotation de la galaxie (logv), et sa vitesse radiale héliocentrique (vrad).

Déterminer la magnitude absolue de M31. Quelle hypothèse fait-on sur les magnitudes absolues de ses sosies ?
Déterminer pour chaque galaxie son module de distance et en déduire la valeur de la constante de Hubble associée :
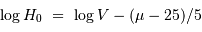
Déterminer le module de distance mu2 par application de la relation de Tully-Fisher, avec les coefficients 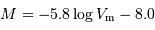 .
En déduire une autre estimation de
.
En déduire une autre estimation de 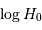 .
.
Calculer dans chaque cas la moyenne des valeurs 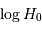 et en déduire une valeur de la constante de Hubble. Commenter.
et en déduire une valeur de la constante de Hubble. Commenter.
Représenter les valeurs 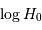 en fonction de la vitesse radiale pour les galaxies sosies de M31. Commenter.
en fonction de la vitesse radiale pour les galaxies sosies de M31. Commenter.
Appliquer la correction de Malmquist et calculer la valeur corrigée de 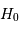 . Comparer aux valeurs obtenues précédemment, par le module de distance ou par la relation Tully-Fisher.
. Comparer aux valeurs obtenues précédemment, par le module de distance ou par la relation Tully-Fisher.
Dans le modèle standard 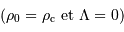 , l'âge de l'univers est égal à 2/3 du temps de Hubble
, l'âge de l'univers est égal à 2/3 du temps de Hubble 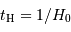 . Calculer cet âge à partir des valeurs de
. Calculer cet âge à partir des valeurs de 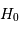 obtenues précédemment. On rappelle que la constante est exprimée en km/s/Mpc.
obtenues précédemment. On rappelle que la constante est exprimée en km/s/Mpc.
Dans un modèle d'univers non-statique à espace temps variable, la loi de Hubble existe, même si toutes les galaxies sont comobiles avec le système de coordonnées, i.e. si leur énergie cinétique est nulle, aux mouvements propres près. La métrique non-statique la plus générale est la métrique de Robertson-Walker qui s'écrit:
![{\mathrm{d}} s^2 = - R(t)^2 \left[ \frac{ {\mathrm{d}} r^2}{1-kr^2} + r^2 ( {\mathrm{d}}\theta^2 + \sin^2\theta {\mathrm{d}}\phi^2) \right] + c^2 {\mathrm{d}} t^2](../pages_indicateur-secondaire/equations_cosmologie/equation1.png)
où 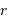 ,
, 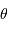 ,
, 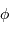 sont les paramètres d'espace et
sont les paramètres d'espace et 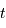 le temps. La fonction
le temps. La fonction 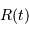 représente le rayon de l'univers à l'instant
représente le rayon de l'univers à l'instant 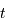 .
.
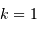 , l'univers est à géométrie sphérique, et
l'espace est fini.
, l'univers est à géométrie sphérique, et
l'espace est fini.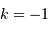 , l'univers est à géométrie hyperbolique, et
l'espace est à chaque instant ouvert et infini.
, l'univers est à géométrie hyperbolique, et
l'espace est à chaque instant ouvert et infini.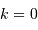 , l'univers est à géométrie parabolique, et
l'espace est aussi ouvert et infini, mais il est à chaque instant
isométrique à un espace plat euclidien.
, l'univers est à géométrie parabolique, et
l'espace est aussi ouvert et infini, mais il est à chaque instant
isométrique à un espace plat euclidien.
C'est la densité massique de l'univers qui détermine son type de géométrie. Une forte densité courbe l'espace au point de le refermer sur lui-même en un modèle sphérique ; toute densité plus faible qu'une certaine densité critique 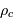 (univers parabolique) conduit à un modèle hyperbolique infini.
La détermination de la fonction de métrique
(univers parabolique) conduit à un modèle hyperbolique infini.
La détermination de la fonction de métrique 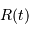 permet de décrire l'évolution de l'univers au cours du temps. L'application des équations d'Einstein à la métrique de Robertson-Walker conduit aux deux équations différentielles suivantes :
permet de décrire l'évolution de l'univers au cours du temps. L'application des équations d'Einstein à la métrique de Robertson-Walker conduit aux deux équations différentielles suivantes :
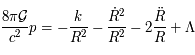
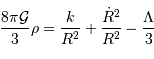
auxquelles on ajoute l'intégrale première:
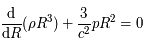
où 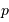 est la pression du fluide de galaxies,
est la pression du fluide de galaxies, 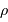 la densité de la matière, et
la densité de la matière, et 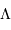 la constante cosmologique.
la constante cosmologique. 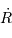 et
et 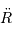 représentent respectivement les dérivées première et seconde du rayon de l'univers
représentent respectivement les dérivées première et seconde du rayon de l'univers 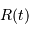 par rapport au temps.
On définit:
par rapport au temps.
On définit:
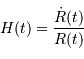 la constante de Hubble à
l'instant
la constante de Hubble à
l'instant 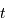 , i.e. le taux d'expansion à l'instant
, i.e. le taux d'expansion à l'instant 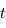 .
.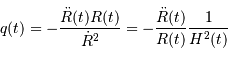 , le paramètre de décélération.
, le paramètre de décélération.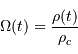 , le paramètre de densité.
, le paramètre de densité.
Si on suppose que l'univers est homogène et isotrope (principe
cosmologique), le modèle est entièrement défini par trois
paramètres : la valeur de la constante cosmologique
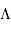 , la valeur actuelle de la constante de Hubble
, la valeur actuelle de la constante de Hubble 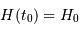 , et la valeur actuelle du paramètre de densité
, et la valeur actuelle du paramètre de densité 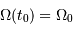 (ou du paramètre de décélération
actuel
(ou du paramètre de décélération
actuel 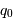 ). On considère généralement que la pression
). On considère généralement que la pression 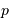 du fluide de galaxie est nulle, ce qui implique d'après les équations (1.1) et (1.2) que
du fluide de galaxie est nulle, ce qui implique d'après les équations (1.1) et (1.2) que 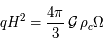 , et donc que
, et donc que 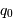 et
et 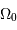 sont interchangeables.
sont interchangeables.
Dans les modèles de Friedman caractérisés par une constante cosmologique nulle (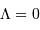 ), l'expansion se ralentit au cours du temps; il en résulte que l'âge
), l'expansion se ralentit au cours du temps; il en résulte que l'âge 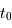 de l'Univers est toujours inférieur au temps de Hubble
de l'Univers est toujours inférieur au temps de Hubble 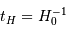 .
.
L'effet Sunyaev Zel'dovich se caractérise pas un déficit de photons du fond diffus cosmologique.
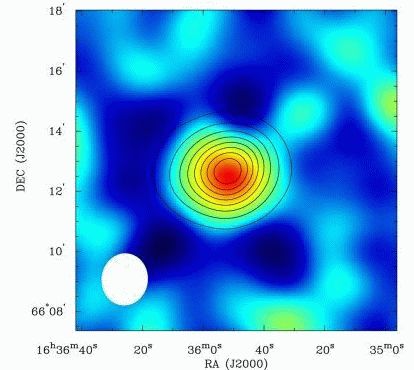
L'effet de lentille gravitationnelle démultiplie spectaculairement les images d'un objet très lointain situé derrière une forte concentration de masse.

A très grande échelle, on fait souvent appel à des propriétés générales des amas de galaxies. Ainsi, un des premiers indicateurs à longue portée utilisé fut la galaxie la plus brillante d'un amas, ou la moyenne des luminosité des 5 galaxies les plus brillantes.
Une autre méthode fait appel à la taille caractéristique des amas de galaxies, qui est de l'ordre de 10 à 20 millions d'années de lumière. On trouve aussi un critère équivalent à la relation de Faber-Jackson pour les amas de galaxies en comparant la luminosité  du gaz chaud du milieu intergalactique à la
dispersion des vitesses des galaxies à l'intérieur de l'amas.
du gaz chaud du milieu intergalactique à la
dispersion des vitesses des galaxies à l'intérieur de l'amas.
Deux autres méthodes très prometteuses ont fait des progrès récents. Il s'agit de l'utilisation de l'effet Sunyaev-Zel'dovich et des lentilles gravitationnelles.
L'effet Sunyaev-Zel'dovich peut être décrit comme l'interaction du plasma d'électron chaud baignant les amas de galaxies avec le fond diffus cosmologique à 2.7 K : les photons froids prennent de l'énergie aux électrons chauds par un effet appelé Compton inverse. Il en résulte que lorsque l'on étudie le fond diffus cosmologique dans la direction d'un amas, on observe un déficit de photons à la température habituelle de ce fond et un excédent de photons plus chauds.
Cette observation permet de mesurer la profondeur de l'amas le long de la ligne de visée de façon indépendante de la distance. En comparant cette mesure à l'image du même amas en rayonnement X, on peut, en supposant que l'amas est sphérique, en déduire sa distance.
L'effet de lentille gravitationnelle est basé sur la déviation de la lumière par la gravitation. Ce principe a été décrit dans la théorie de la relativité générale. L'utilisation des lentilles gravitationnelles repose sur la mesure des délais temporels entre les différentes images d'une même source dont le trajet des rayons lumineux a été perturbée par un fort potentiel gravitationnel comme par exemple celui d'un amas de galaxies. Si l'on est capable de modéliser la distribution de la masse dans l'amas déflecteur en question, on peut alors estimer la distance de la source.
Au terme de cette revue des méthodes de détermination des distances dans l'univers, on peut se demander pourquoi on continue de perfectionner ces techniques si compliquées et indirectes, alors que, pour les galaxies, la loi de Hubble et les mesures du décalage vers le rouge seules suffiraient...
En fait, en mesurant de manière indépendante la distance des galaxies (à partir d'indicateurs photométriques) et leur vitesse radiale (à partir de mesures spectroscopiques), on peut accéder à des paramètres d'importance cosmologique comme :
pages_loi-hubble/loi-hubble-sexercer.html
pages_indicateur-secondaire/statistique-global-sexercer.html
Résultats :
| PGC | 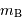 |  (deg) (deg) | largeur (km/s) |
| 49157 | 13.03 | 66.6 | 340 |
| 49322 | 15.20 | 67.8 | 255 |
| 49275 | 13.34 | 64.1 | 430 |
| 48925 | 15.23 | 82.3 | 200 |
Estimer le rôle de la turbulence sur la raie, ainsi que celui de la projection.
La composante de la turbulence est à soustraire. Le facteur de déprojection est 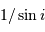 .
.
La largeur totale compte 2 fois la rotation
Pour passer de la largeur totale de la raie à la vitesse maximale, il faut tenir compte que la raie est élargie par les vitesses se rapprochant et s'éloignant de l'observateur. D'où les facteurs 2 dans la relation qui suit :
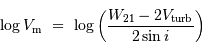
pour calculer les 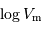 .
.
| PGC | 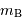 |  (deg) (deg) | largeur (km/s) | 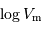 |
| 49157 | 13.03 | 66.6 | 340 | 2.21 |
| 49322 | 15.20 | 67.8 | 255 | 2.06 |
| 49275 | 13.34 | 64.1 | 430 | 2.33 |
| 48925 | 15.23 | 82.3 | 200 | 1.91 |
pages_indicateur-secondaire/statistique-global-sexercer.html
Ouvrir le tableau d'une part, l'une des 2 images de l'autre. Y lire les coordonnées des objets.
Les étoiles brillantes, objets ponctuels, sont accompagnées d'une belle figure de diffraction. Ne pas les traiter.
L'unité des paramètres angulaires est visiblement le degré, pa variant de 0 à 180 deg, et i de 0 à 90.
Les objets caractérisés par une petite valeur de i semblent vus de face ; ceux pour lesquels ce paramètre tend vers 90 deg sont plutôt vus par la tranche : i représente l'inclinaison.
Les objets avec une valeur faible de pa (p.ex. PGC 49514) semblent avoir des axes principaux alignés avec ceux de la carte ; un objet avec pa de l'ordre de 45 deg (p.ex. PGC 49347) est globalement "en diagonale" par rapport aux axes de position et un autre objet avec pa de l'ordre de 134 deg (p.ex. PGC 49356) lui est orthogonal : pa représente le paramètre angulaire, à savoir l'orientation des axes.
Les figures des questions suivantes proposent quelques identifications.
L'inclinaison de PGC 49354 vaut 23.3 deg ; celle de PGC 49389 vaut 90.0 deg.
Comment reconnaître si elles sont proches selon la dimension radiale perpendiculaire au plan du ciel ?
Ces galaxies sont proches en ascension droite et déclinaison. Elles doivent également être proches selon la 3e dimension, vu que leurs vitesses de fuite par rapport au Soleil apparaissent très voisines (2300 et 2450 km/s).
Le fait d'avoir ces objets sur une même carte indique leur proximité dans le plan du ciel. Comment estimer leur éloignement ?
Un groupe d'objets va se caractériser par des vitesses radiales héliocentriques voisines. On repère donc les groupes par leur vitesse radiale. La représenter en fonction de l'une des coordonnées angulaires ou de la magnitude apparente.
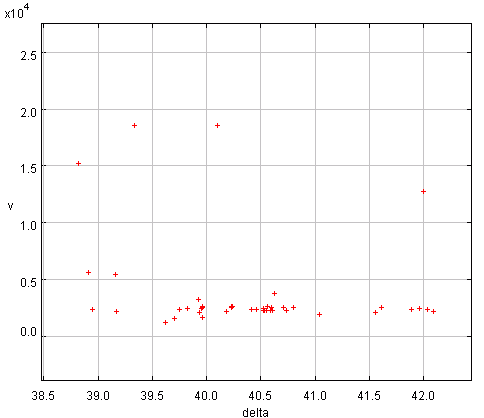
Avec le critère sur la vitesse radiale héliocentrique, et en représentant cette vitesse en fonction d'une variable angulaire de position ou de la magnitude, on identifie différents groupes :
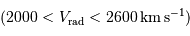 , avec plus de 30 composantes.
, avec plus de 30 composantes.pages_indicateur-secondaire/statistique-global-sexercer.html
Réfléchir aux propriétés que doit avoir la galaxie.
Identifier les données nécessaires.
En ce qui concerne l'inclinaison, quelle mesure doit être possible, et qu'est-ce que cela implique ?
Critère sur les objets : il faut sélectionner, parmi la base de données, les galaxies de type spirale, appartenant à l'amas. On exclut donc les irrégulières, celles dont le type n'est pas défini, et celles dont la vitesse radiale est très différente de celle de NGC 5350.
Critère sur les mesures : il faut bien sur que les galaxies possèdent une mesure de 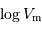 ainsi qu'une magnitude. On exclut celles qui ne satisfont pas à ces critères.
ainsi qu'une magnitude. On exclut celles qui ne satisfont pas à ces critères.
Mesure de la vitesse de rotation : les galaxies ne doivent pas être vues de face afin que la mesure de vitesse de rotation par effet Doppler soit possible.
Avec ces critères quantifiés, il ne reste finalement qu'une douzaine d'objets (cf. tableau à la question suivante).
Dans quel sens l'extinction agit-elle ?
La correction des effets d'extinction est :
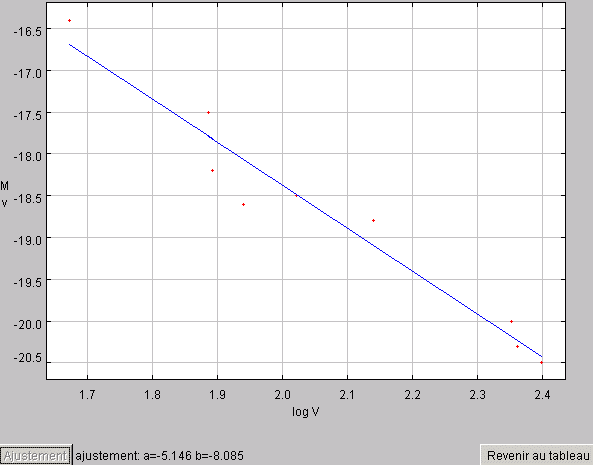
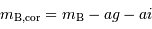 Afficher le graphe de mbc fonction de logvrot, et puis se servir de la fonction ajustement.
Afficher le graphe de mbc fonction de logvrot, et puis se servir de la fonction ajustement.
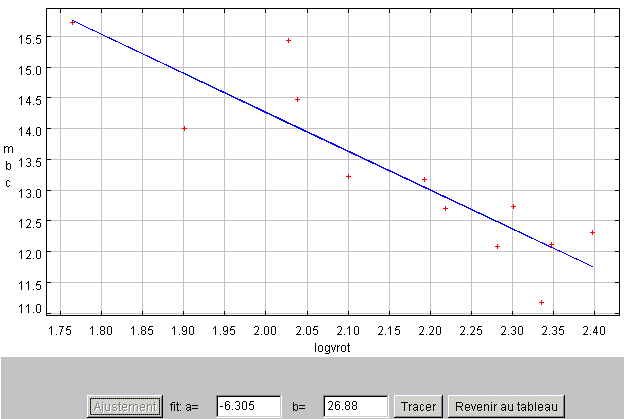
L'estimation linéaire conduit à une pente de -6.3 et une ordonnée à l'origine de 26.9
Afficher le graphe de mbc fonction de logvrot, forcer le paramètre a à la valeur -5.8, choisir une valeur pour b et ajuster au mieux "à la main".
Un point apparaît hors norme dans l'estimation (PGC 49480). On l'élimine dans le tableau en remplaçant p.ex. sa magnitude mbc par un blanc. On trouve alors l'estimation avec une pente de -5.83 et une ordonnée à l'origine de 25.7.
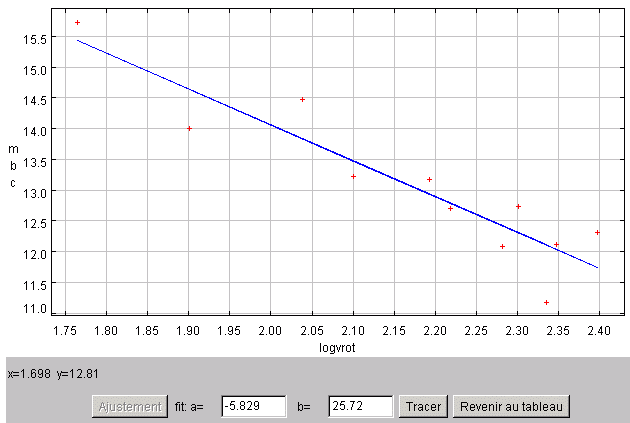
En forçant la pente à -5.8, le coefficient à l'origine est de l'ordre de 25.6.
Si besoin, réviser la notion de module de distance.
L'estimation sur les données a conduit à une ordonnée à l'origine de +25.6, pour la magnitude apparente, contre -8 pour la magnitude absolue. Le module de distance vaut donc 33.6. On en déduit, par application de la relation
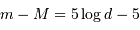 que la distance
que la distance 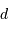 vaut 52 Mpc.
vaut 52 Mpc.
Application de la relation de Hubble : 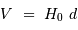
La valeur moyenne des vitesses est de l'ordre de 2400 km/s.
L'application de la relation de Hubble 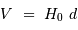 donne
donne 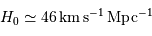 .
.
pages_indicateur-secondaire/biais-malmquist-sexercer.html
La magnitude apparente de M31 et son module de distance sont donnés.
M31 = PGC 2557
Par application de la relation donnant le module de distance :
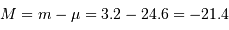
Toutes les galaxie sosies de M31 sont supposées avoir la même magnitude absolue.
A l'aide de l'appliquette, calculer le module de distance mu1.
Toujours à l'aide de l'appliquette, déduire 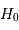 (log(H01)) du module de distance mu1.
(log(H01)) du module de distance mu1.
Le calcul, via l'appliquette, du module de distance est immédiat.
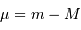 , avec
, avec 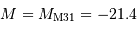 (sélectionner la case F1 et taper la commande = B1 + 21.4 ou bien
= mb + 21.4).
(sélectionner la case F1 et taper la commande = B1 + 21.4 ou bien
= mb + 21.4).
Ensuite, on déduit 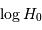 par la relation demandée
(sélectionner la case H1 et taper la commande = log(E1) - (F1-25)/5. ou bien = log(vrad) - (mu1-25)/5). Attention à sélectionner la bonne vitesse (vrad : vitesse radiale héliocentrique).
par la relation demandée
(sélectionner la case H1 et taper la commande = log(E1) - (F1-25)/5. ou bien = log(vrad) - (mu1-25)/5). Attention à sélectionner la bonne vitesse (vrad : vitesse radiale héliocentrique).
En appliquant la relation de Tully-Fisher pour le module de distance,
on calcule 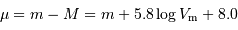 (via la sélection de G1 et =mb+5.8*logv+8).
(via la sélection de G1 et =mb+5.8*logv+8).
Ensuite, on déduit 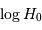 par la relation demandée
(sélectionner la case I1 et taper la commande =log(E1)-(G1-25)/5. ou bien =log(vrad) -(mu2-25)/5).
par la relation demandée
(sélectionner la case I1 et taper la commande =log(E1)-(G1-25)/5. ou bien =log(vrad) -(mu2-25)/5).
Estimer la moyenne en représentant 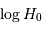 en fonction de PGC.
en fonction de PGC.
Pour la valeur log(H01), on estime la moyenne à 1.65, pour log(H02), elle vaut plutôt 1.55.
On s'aperçoit que  augmente avec la vitesse radiale, et donc avec la distance. Ceci est incompatible avec la relation linéaire énoncée par la loi de Hubble. Mais l'effet n'est pas réel ; il provient du biais induit par la coupure en magnitude à grande distance.
augmente avec la vitesse radiale, et donc avec la distance. Ceci est incompatible avec la relation linéaire énoncée par la loi de Hubble. Mais l'effet n'est pas réel ; il provient du biais induit par la coupure en magnitude à grande distance.
Voir le cours.
La correction de Malmquist revient à corriger 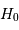 à la baisse de 23%. On obtient donc, de
à la baisse de 23%. On obtient donc, de 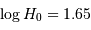 , la valeur non corrigée d'environ 44 km/s/Mpc, qui devient après correction environ 33 km/s/Mpc.
, la valeur non corrigée d'environ 44 km/s/Mpc, qui devient après correction environ 33 km/s/Mpc.
Convertir les unités km/s/Mpc en l'inverse d'un temps.
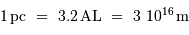 .
.
La définition du temps de Hubble est :
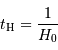
L'unité à traiter est le Mpc/km s. Comme
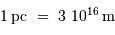 ,
,
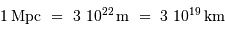 .
Par ailleurs,
.
Par ailleurs, 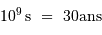 .
.
On en déduit le temps de Hubble, de l'ordre de 27 milliards d'années, d'où l'âge de l'Univers de l'ordre de 18 milliards d'années dans le cadre de ce modèle.