Magnitude apparente
Etoile double du Bouvier

L'étoile centrale a une magnitude de 4,5, la seconde étoile a une magnitude de 7,2 et les étoiles du fond de ciel une magnitude comprise entre 15 et 18.
Crédit :
CDS
La magnitude apparente mesure l'"éclat" apparent d'une étoile, c'est à dire la façon dont on la voit de la Terre.
Quelques magnitudes apparentes
| Objet | Magnitude apparente |
|---|
| Soleil | -26,7 |
| Lune | -12,7 |
| Vénus | -4,4 |
| Sirus | -1,4 |
| Véga | 0 |
| Antarès | 1 |
| Etoile polaire | 2 |
| Limite de perception à l'oeil nu | 6 |
| Limite de perception aux jumelles | 10 |
| Limite de perception au sol | 27 |
| Limite de perception du télescope spatial Hubble | 30 |
Plus un objet est brillant, plus sa magnitude est petite. Une
différence de magnitude de 2.5 unités correspond à un contraste de
luminosité de 10.
Magnitude apparente
 Définition
Définition
La magnitude est une grandeur qui permet de mesurer la luminosité des astres.
La magnitude apparente 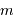 d'une étoile est définie conventionnellement à partir de son flux
d'une étoile est définie conventionnellement à partir de son flux 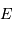 par la relation :
par la relation :
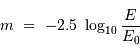
où 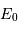 représente le flux
d'une étoile de référence de magnitude nulle.
représente le flux
d'une étoile de référence de magnitude nulle.
Le facteur 2.5 et la base logarithmique décimale ont été choisis afin de respecter la définition historique.
La définition du flux ici introduit n'est pas primordiale, vu que la définition se contente d'introduire un rapport de cette grandeur. On peut se référer à un tableau récapitulatif des grandeurs photométriques utilisées.
La différence de magnitude de deux étoiles, 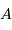 et
et 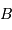 , s'exprime par :
, s'exprime par :
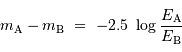
Elle est égale à 2.5 en valeur absolue si le rapport de leurs flux est 10.
D'autres échelles de magnitude
La magnitude apparente ne nous renseigne en rien sur la luminosité réelle de l'astre et ne donne aucune indication sur sa nature, car la définition de la magnitude apparente :
- ne dépend pas a priori du récepteur utilisé,
- ne dépend que de l'éclat apparent de l'objet et donc mélange une information propre à l'étoile (son flux) à la distance Terre-étoile,
- ne tient pas compte de la couleur de l'étoile,
- ne nécessite pas une définition précise de la grandeur photométrique mesurée, vu que seul le rapport de deux telles grandeurs entre en jeu.
Des définitions plus circonstanciées permettent de préciser la notion de magnitude.
On introduit la magnitude absolue 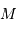 , qui indique la luminosité d'un objet rapporté à une distance de 10 parsec.
, qui indique la luminosité d'un objet rapporté à une distance de 10 parsec.
De même, la définition précédente néglige toute information sur la couleur de l'objet. Pour cela, on introduit la magnitude monochromatique et les indices de couleur.
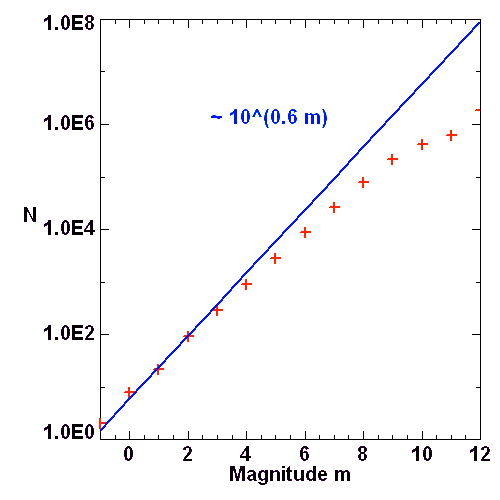
Décompte des cibles stellaires jusqu'à la magnitude 12. La loi en
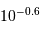
n'est plus vérifiée à grande distance, l'absorption interstellaire et la taille finie de l'épaisseur du bras galactique conduisant à un déficit de magnitudes faibles.
Crédit :
ASM
 Luminosité et éclairement
Luminosité et éclairement
Difficulté : ☆
Temps : 10 min
La luminosité correspond à la puissance totale rayonnée par l'étoile.
Lorsque cette puissance est considérée par unité de surface, on parle
de puissance surfacique. On définit l'éclairement 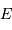 d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
Question 2)
Calculer la puissance surfacique reçue
sur Terre d'une étoile de type solaire située à la distance de Proxima
de Centaure, de parallaxe annuelle 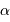 = 0.76". On donne
= 0.76". On donne 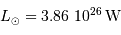 .
.
Question 3)
De même, calculer la puissance surfacique
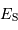 du Soleil reçu sur Terre.
du Soleil reçu sur Terre.
 Magnitude apparente
Magnitude apparente
Difficulté : ☆
Temps : 15 min
Question 1)
Rappeler la définition de la magnitude apparente d'une étoile.
Question 2)
Deux étoiles ont des éclairements apparents 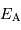 et
et 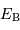 . Exprimer leur différence de magnitude.
. Exprimer leur différence de magnitude.
Question 3)
Comparer les flux d'objets de magnitudes -26.7 (soleil), -2.55 (Jupiter), +6 (étoiles juste visibles à l'oeil nu), +27 (magnitude limite accessible au sol).
 Performance de détection liée à la taille du récepteur
Performance de détection liée à la taille du récepteur
Difficulté : ☆
Temps : 25 min
En vision nocturne, le diamètre de notre pupille vaut de l'ordre de 6 mm, et la magnitude limite visible à l'oeil nu est 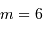 .
.
On rappelle l'expression de 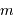 , la magnitude apparente d'un objet :
, la magnitude apparente d'un objet :
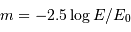
avec 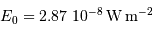 pour le domaine visible.
pour le domaine visible.
Question 1)
Exprimer 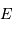 , le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de
, le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de 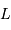 et
et 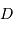 , respectivement la puissance totale reçue et le diamètre de la pupille.
, respectivement la puissance totale reçue et le diamètre de la pupille.
Par définition, l'éclairement découle de la luminosité :
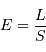
Question 2)
Calculer 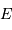 et
et 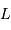 pour une étoile de magnitude 6.
pour une étoile de magnitude 6.
Question 3)
Montrer qu'avec un collecteur de diamètre 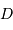 , l'oeil a accès aux magnitudes jusqu'à :
, l'oeil a accès aux magnitudes jusqu'à :
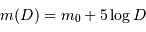
avec 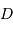 exprimé en m. Identifier
exprimé en m. Identifier 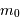
Question 4)
Calculer 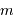 , pour
, pour 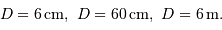
Question 5)
Comment procède-t-on pour observer les objets de magnitude supérieure?
 Compter les étoiles
Compter les étoiles
Difficulté : ☆
Temps : 20 min
Le but de cet exercice est de compter les étoiles en fonction de leur
magnitude. Pour se faire, on pose deux hypothèses :
- toutes les étoiles présentent la même magnitude absolue,
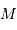 .
. - la répartition des étoiles autour du soleil est uniforme,
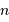 .
.
Question 1)
Déterminer la magnitude apparente d'une étoile à la distance 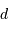 .
.
Revoir le cours, et la définition
de la magnitude absolue.
Question 2)
Dénombrer le nombre d'étoiles 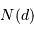 dans une sphère de rayon
dans une sphère de rayon 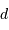 autour du
soleil.
autour du
soleil.
Le volume d'une sphère de rayon 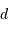 est... allons, un petit effort
est... allons, un petit effort
...
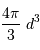
Question 3)
A partir des deux relations précédemment établies, montrer que le nombre
d'étoiles jusqu'à la magnitude 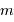 évolue comme :
évolue comme :
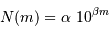
Identifier le coefficient 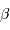 de l'exposant
de l'exposant
Eliminer la variable 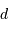 des équations précédentes
des équations précédentes
D'après ce qui précède, le rayon 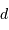 , exprimé en parsec, s'exprime en fonction des magnitudes par
, exprimé en parsec, s'exprime en fonction des magnitudes par
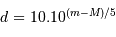
Question 4)
Estimer 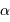 , sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
, sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
Question 5)
Ce résultat apparaît-il en accord avec le nombre d'étoiles plus brillantes que la magnitude 0
 Différence de magnitude
Différence de magnitude
Difficulté : ☆
Temps : 20 min
Question 1)
Deux étoiles d'un système double présentent une différence de magnitude
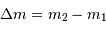 .
Exprimer le rapport de leurs luminosités
.
Exprimer le rapport de leurs luminosités 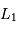 et
et 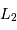
[2 points]
Question 2)
Faire l'application numérique pour 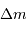 = 1,
= 1, 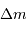 = 10
= 10
[1 points]
 Le projet OWL
Le projet OWL
Difficulté : ☆
Temps : 20 min
Le projet OWL (overwhelmingly large telescope) de l'ESO s'est attaché à étudier le concept d'un télescope avec un collecteur de diamètre 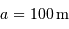 . Devant l'accumulation de points durs techniques, le concept a été remplacé en 2006 par un projet moins démesuré, avec un collecteur de diamètre 42 m.
. Devant l'accumulation de points durs techniques, le concept a été remplacé en 2006 par un projet moins démesuré, avec un collecteur de diamètre 42 m.
Question 1)
Estimer le gain attendu en magnitude limite observable avec un télescope de 100 m, par rapport à un télescope de 10 m.
[1 points]
Question 2)
Ce télescope étant muni d'une optique adaptative, il donnera accès à une résolution angulaire proche de la limite de diffraction 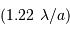 . Calculer cette limite pour le visible.
. Calculer cette limite pour le visible.
[1 points]
- Question 1
Aide :
Par définition, l'éclairement découle de la luminosité :
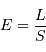
Solution :
Par définition, l'éclairement découle de la luminosité :
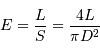
- Question 2
Solution :
La définition de la magnitude,
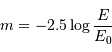 ,
conduit à :
,
conduit à :
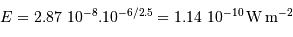
D'où la luminosité :
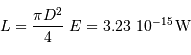
- Question 3
Solution :
On applique la définition, avec le flux 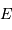 identiquement égal à
identiquement égal à 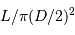 .
.
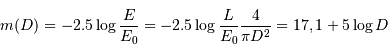
- Question 4
Solution :
L'application numérique donne :
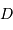 | 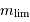 |
| 6 cm | 11 |
| 60 cm | 16 |
| 6 m | 21 |
(mais un télescope de 6 m n'est pas conçu pour se rincer l'oeil).
- Question 5
Solution :
Pour qu'une étoile soit visible, il faut que suffisamment de photons émis par celle-ci arrivent à l'observateur pendant un laps de temps. Pour voir des objets peu lumineux, il est alors nécessaire d'augmenter le temps de pose des instruments de mesure.
- Question 1
Aide :
Revoir le cours, et la définition
de la magnitude absolue.
Solution :
Par définition de la magnitude absolue :
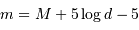
- Question 2
Aide :
Le volume d'une sphère de rayon 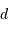 est... allons, un petit effort
est... allons, un petit effort
Aide :
...
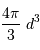
Solution :
Le volume de la sphère de rayon 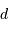 multiplié par la densité stellaire donne le nombre d'étoiles :
multiplié par la densité stellaire donne le nombre d'étoiles :
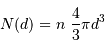
- Question 3
Aide :
Eliminer la variable 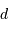 des équations précédentes
des équations précédentes
Aide :
D'après ce qui précède, le rayon 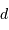 , exprimé en parsec, s'exprime en fonction des magnitudes par
, exprimé en parsec, s'exprime en fonction des magnitudes par
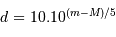
Solution :
De 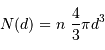 et
et
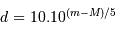 , il sort immédiatement :
, il sort immédiatement :
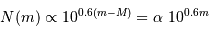
- Question 4
Solution :
Il s'agit pour 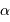 de vérifier :
de vérifier :
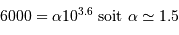
- Question 5
Solution :
Le facteur 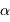 s'identifie à
s'identifie à 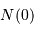 , nombre d'étoiles de magnitude
inférieure à
, nombre d'étoiles de magnitude
inférieure à 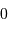 . Si l'on se réfère au
tableau, recensant les objets les plus
brillants, l'ordre de grandeur est correct.
. Si l'on se réfère au
tableau, recensant les objets les plus
brillants, l'ordre de grandeur est correct.

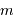 d'une étoile est définie conventionnellement à partir de son flux
d'une étoile est définie conventionnellement à partir de son flux 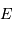 par la relation :
par la relation :
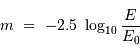
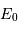 représente le flux
d'une étoile de référence de magnitude nulle.
représente le flux
d'une étoile de référence de magnitude nulle.
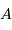 et
et 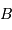 , s'exprime par :
, s'exprime par :
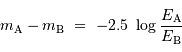
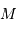 , qui indique la luminosité d'un objet rapporté à une distance de 10
, qui indique la luminosité d'un objet rapporté à une distance de 10 
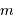 , décompte du nombre
, décompte du nombre 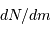 d'étoiles de magnitude comprise dans l'intervalle
d'étoiles de magnitude comprise dans l'intervalle ![[m-0.5, m+0.5]](../pages_luminosite/equations_magnitude-apparente/equation11.png) , et total cumulé
, et total cumulé 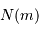 jusqu'à la magnitude
jusqu'à la magnitude 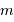 .
.
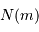 , et à montrer qu'elle est
du type :
, et à montrer qu'elle est
du type :
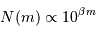
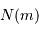 observables jusqu'à une
magnitude apparente donnée
observables jusqu'à une
magnitude apparente donnée 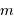 , puis
, puis 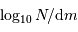 en fonction de
en fonction de 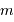 (
(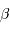 graphiquement, et montrer que
graphiquement, et montrer que 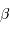 est voisin de 0.6
est voisin de 0.6
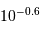 n'est plus vérifiée à grande distance, l'absorption interstellaire et la taille finie de l'épaisseur du bras galactique conduisant à un déficit de magnitudes faibles.
n'est plus vérifiée à grande distance, l'absorption interstellaire et la taille finie de l'épaisseur du bras galactique conduisant à un déficit de magnitudes faibles.
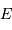 d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
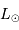 , en
déduire l'éclairement
, en
déduire l'éclairement 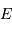 de cette étoile située à une distance
de cette étoile située à une distance 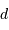 de la Terre.
de la Terre.
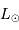 est une puissance et
est une puissance et 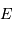 une puissance surfacique
une puissance surfacique
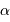 = 0.76". On donne
= 0.76". On donne 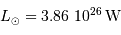 .
.
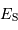 du Soleil reçu sur Terre.
du Soleil reçu sur Terre.
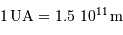
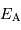 et
et 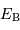 . Exprimer leur différence de magnitude.
. Exprimer leur différence de magnitude.
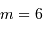 .
.
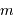 , la magnitude apparente d'un objet :
, la magnitude apparente d'un objet :
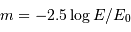
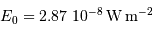 pour le domaine visible.
pour le domaine visible.
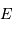 , le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de
, le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de 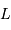 et
et 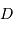 , respectivement la puissance totale reçue et le diamètre de la pupille.
, respectivement la puissance totale reçue et le diamètre de la pupille.
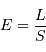
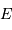 et
et 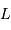 pour une étoile de magnitude 6.
pour une étoile de magnitude 6.
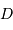 , l'oeil a accès aux magnitudes jusqu'à :
, l'oeil a accès aux magnitudes jusqu'à :
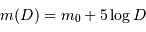
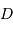 exprimé en m. Identifier
exprimé en m. Identifier 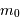
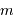 , pour
, pour 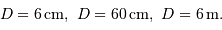
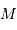 .
.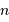 .
.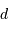 .
.
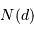 dans une sphère de rayon
dans une sphère de rayon 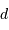 autour du
soleil.
autour du
soleil.
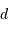 est... allons, un petit effort
est... allons, un petit effort
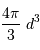
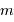 évolue comme :
évolue comme :
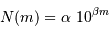
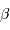 de l'exposant
de l'exposant
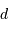 des équations précédentes
des équations précédentes
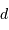 , exprimé en parsec, s'exprime en fonction des magnitudes par
, exprimé en parsec, s'exprime en fonction des magnitudes par
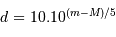
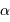 , sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
, sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
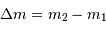 .
Exprimer le rapport de leurs luminosités
.
Exprimer le rapport de leurs luminosités 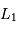 et
et 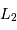
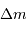 = 1,
= 1, 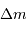 = 10
= 10
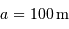 . Devant l'accumulation de points durs techniques, le concept a été remplacé en 2006 par un projet moins démesuré, avec un collecteur de diamètre 42 m.
. Devant l'accumulation de points durs techniques, le concept a été remplacé en 2006 par un projet moins démesuré, avec un collecteur de diamètre 42 m.
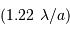 . Calculer cette limite pour le visible.
. Calculer cette limite pour le visible.
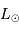 est uniformément répartie sur la sphère de rayon
est uniformément répartie sur la sphère de rayon
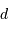 :
:
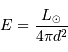
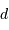 :
:
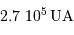 .
.
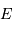 :
:
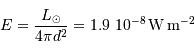
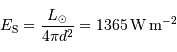
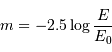
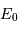 est l'éclairement apparent de référence.
est l'éclairement apparent de référence.
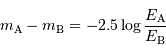
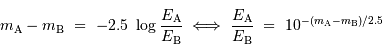
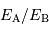 )
)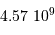
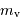 = 6
= 6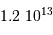
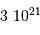
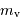 = 6
= 6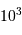
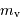 = 6
= 6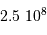
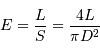
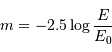 ,
conduit à :
,
conduit à :
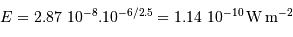
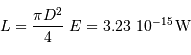
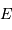 identiquement égal à
identiquement égal à 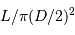 .
.
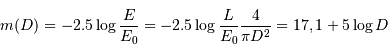
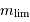
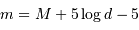
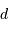 multiplié par la densité stellaire donne le nombre d'étoiles :
multiplié par la densité stellaire donne le nombre d'étoiles :
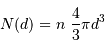
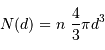 et
et
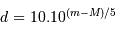 , il sort immédiatement :
, il sort immédiatement :
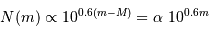
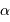 de vérifier :
de vérifier :
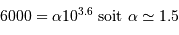
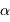 s'identifie à
s'identifie à 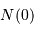 , nombre d'étoiles de magnitude
inférieure à
, nombre d'étoiles de magnitude
inférieure à 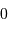 . Si l'on se réfère au
. Si l'on se réfère au