
|
Difficulté : ☆ Temps : 10 min
La luminosité correspond à la puissance totale rayonnée par l'étoile.
Lorsque cette puissance est considérée par unité de surface, on parle
de puissance surfacique. On définit l'éclairement 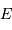 d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
La luminosité intrinsèque d'une étoile de type solaire étant 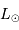 , en
déduire l'éclairement
, en
déduire l'éclairement 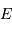 de cette étoile située à une distance
de cette étoile située à une distance 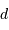 de la Terre.
de la Terre.
Calculer la puissance surfacique reçue
sur Terre d'une étoile de type solaire située à la distance de Proxima
de Centaure, de parallaxe annuelle 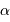 = 0.76". On donne
= 0.76". On donne 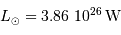 .
.
Difficulté : ☆ Temps : 15 min
Deux étoiles ont des éclairements apparents 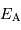 et
et 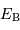 . Exprimer leur différence de magnitude.
. Exprimer leur différence de magnitude.
Comparer les flux d'objets de magnitudes -26.7 (soleil), -2.55 (Jupiter), +6 (étoiles juste visibles à l'oeil nu), +27 (magnitude limite accessible au sol).
Difficulté : ☆ Temps : 25 min
En vision nocturne, le diamètre de notre pupille vaut de l'ordre de 6 mm, et la magnitude limite visible à l'oeil nu est 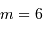 .
.
On rappelle l'expression de 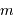 , la magnitude apparente d'un objet :
, la magnitude apparente d'un objet :
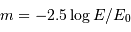
avec 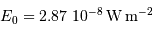 pour le domaine visible.
pour le domaine visible.
Exprimer 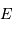 , le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de
, le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de 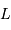 et
et 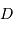 , respectivement la puissance totale reçue et le diamètre de la pupille.
, respectivement la puissance totale reçue et le diamètre de la pupille.
Calculer 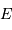 et
et 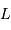 pour une étoile de magnitude 6.
pour une étoile de magnitude 6.
Montrer qu'avec un collecteur de diamètre 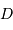 , l'oeil a accès aux magnitudes jusqu'à :
, l'oeil a accès aux magnitudes jusqu'à :
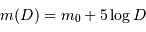
avec 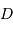 exprimé en m. Identifier
exprimé en m. Identifier 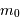
Calculer 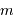 , pour
, pour 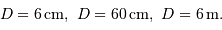
Comment procède-t-on pour observer les objets de magnitude supérieure?
Difficulté : ☆ Temps : 20 min
Le but de cet exercice est de compter les étoiles en fonction de leur magnitude. Pour se faire, on pose deux hypothèses :
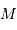 .
.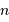 .
.
Dénombrer le nombre d'étoiles 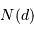 dans une sphère de rayon
dans une sphère de rayon 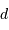 autour du
soleil.
autour du
soleil.
A partir des deux relations précédemment établies, montrer que le nombre
d'étoiles jusqu'à la magnitude 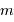 évolue comme :
évolue comme :
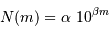
Identifier le coefficient 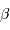 de l'exposant
de l'exposant
Estimer 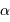 , sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
, sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
Ce résultat apparaît-il en accord avec le nombre d'étoiles plus brillantes que la magnitude 0