
|
Difficulté : ☆☆ Temps : 30 min
On exprime l'ordre de grandeur du module du champ de marée 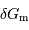 de la Lune sur la Terre de la façon suivante :
de la Lune sur la Terre de la façon suivante :
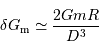
avec 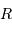 le rayon de la Terre,
le rayon de la Terre, 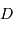 , la distance Terre-Lune (
, la distance Terre-Lune (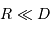 ), et
), et 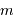 la masse de la Lune.
la masse de la Lune.
Dans le modèle de l'océan global, caractérisé par une distance 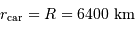 mesurant l'étendue d'eau, la hauteur
mesurant l'étendue d'eau, la hauteur 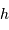 de la
marée est de l'ordre de 1 m.
de la
marée est de l'ordre de 1 m.
En supposant que 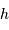 est, comme le champ de marée, une fonction
linéaire de
est, comme le champ de marée, une fonction
linéaire de 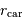 , estimer la hauteur de marée dans les cas suivants :
, estimer la hauteur de marée dans les cas suivants :
En déduire pourquoi il n'y a pas de marée dans une flaque d'eau, ni même dans un grand lac.
On souhaite retrouver l'expression du champ de marée 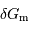 de la
Lune sur la Terre.
de la
Lune sur la Terre.
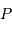 et
et 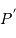 de la Terre, tels que
de la Terre, tels que 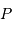 ,
, 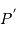 et
et 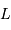 soient alignés, le point
soient alignés, le point 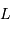 repérant le centre de la Lune.
Soit
repérant le centre de la Lune.
Soit 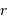 la distance
la distance 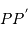 , et
, et 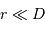 .
.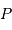 et
et 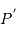 de façon à bien caractériser le problème.
de façon à bien caractériser le problème.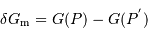 , en effectuant un développement limité au 1er ordre en
, en effectuant un développement limité au 1er ordre en 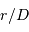 .
.