La marée haute suit la position apparente de la Lune ; marée haute et basse s'alternent rapidement, essentiellement à cause du mouvement de rotation propre de la Terre. Les coefficients de marée sont plus forts dans les conditions d'alignement du Soleil et du couple Terre-Lune, donc aux nouvelle et pleine lunes (modèle statique). Dans un modèle dynamique (plus réaliste), il y a un décalage entre la position de la lune et la marée.
Crédit :
ASM
Bourrelets (é)mouvants
Les animations, dans le cadre d'une théorie statique de la marée et du modèle de l'océan global, montrent comment les
bourrelets de la marée suivent la course de la Lune autour de la Terre.
Horaires de la Lune et des marées
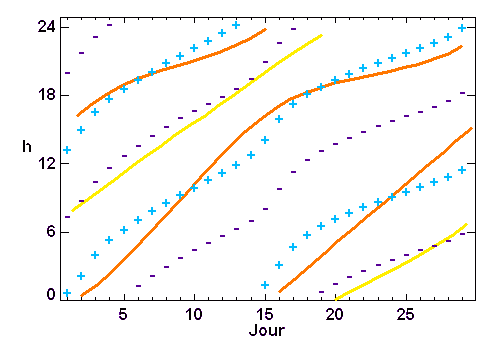
La courbe jaune représente le passage de la Lune au
méridien, et les 2 courbes rouges les levers et couchers de la Lune. Les + et les - signalent respectivement les horaires des marées hautes et basses.
Le modèle statique prévoit la concordance entre marée haute et passage de la Lune au méridien (modulo 12h25), et marée basse et lever ou coucher de la Lune. Ce n'est visiblement pas le cas : les phénomènes dynamiques gouvernent la ... dynamique des marées.
Crédit :
SHOM et ASM
L'approche statique en défaut
L'approche statique suppose que les masses océaniques réagissent instantanément au champ de marée, ce qui n'est pas vrai, comme cela apparaît sur les prévisions. Les conditions géographiques locales entraînent un horaire des marées également local.
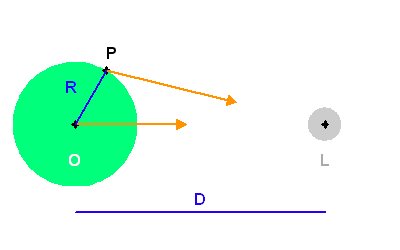
Définitions des distances
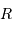
et
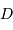
.
Crédit :
ASM
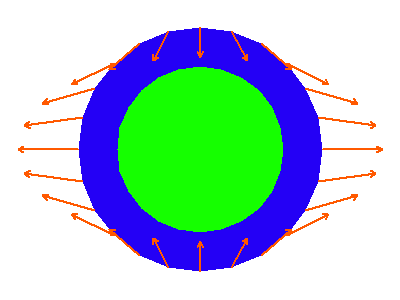
Les forces de marée sont des forces différentielles
La Terre n'est pas un point, mais a une dimension finie. Or l'intensité du champ gravitationnel de la Lune varie comme l'inverse du carré de la distance à la Lune. Il en résulte une attraction différentielle qui déforme la Terre.
On peut estimer la valeur du champ de marée 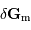 dans le cadre du modèle de l'océan global. On démontre que le module de
dans le cadre du modèle de l'océan global. On démontre que le module de 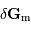 est de l'ordre de
est de l'ordre de 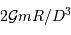
Il ressort de cette analyse que l'effet de marée :
 Marée dans une flaque d'eau
Marée dans une flaque d'eau
Difficulté : ☆☆
Temps : 30 min
Question 1)
On exprime l'ordre de grandeur du module du champ de marée 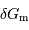 de la Lune sur la Terre de la façon suivante :
de la Lune sur la Terre de la façon suivante :
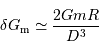
avec 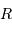 le rayon de la Terre,
le rayon de la Terre, 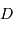 , la distance Terre-Lune (
, la distance Terre-Lune (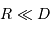 ), et
), et 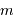 la masse de la Lune.
la masse de la Lune.
Dans le modèle de l'océan global, caractérisé par une distance 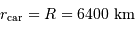 mesurant l'étendue d'eau, la hauteur
mesurant l'étendue d'eau, la hauteur 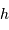 de la
marée est de l'ordre de 1 m.
de la
marée est de l'ordre de 1 m.
En supposant que 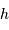 est, comme le champ de marée, une fonction
linéaire de
est, comme le champ de marée, une fonction
linéaire de 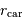 , estimer la hauteur de marée dans les cas suivants :
, estimer la hauteur de marée dans les cas suivants :
- une mer s'étendant sur 640 km,
- un lac s'étendant sur 64 km,
- une flaque d'eau de 64 cm.
En déduire pourquoi il n'y a pas de marée dans une flaque d'eau, ni même dans un grand lac.
[2 points]
Il s'agit d'une règle de trois.


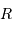 et
et 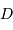 .
.
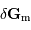 dans le cadre du modèle de l'océan global. On démontre que le module de
dans le cadre du modèle de l'océan global. On démontre que le module de 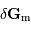 est de l'ordre de
est de l'ordre de 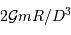
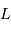 en un point courant
en un point courant 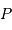 du globe terrestre, que l'on repère par rapport au
centre
du globe terrestre, que l'on repère par rapport au
centre 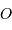 de la Terre.
On note
de la Terre.
On note 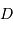 la distance
la distance 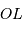 , et
, et 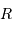 le rayon terrestre.
La composante du champ de marée
le rayon terrestre.
La composante du champ de marée 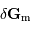 en
en 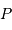 représente la différence du champ lunaire
entre les points
représente la différence du champ lunaire
entre les points 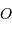 et
et 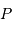 . Les calculs sont menés au 1er ordre par rapport au petit terme
. Les calculs sont menés au 1er ordre par rapport au petit terme 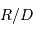 (car
(car 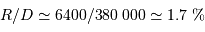 ) :
) :
![\begin{eqnarray*} \delta \mathbf{G} _{\mathrm{m}} &=& {{\cal G} m} { {\mathbf{PL}} \over PL^{3}} - {{\cal G} m} { {\mathbf{OL}} \over OL^{3}} \\ &=& {{\cal G} m} \left[{ {\mathbf{PO}}+ {\mathbf{OL}} \over PL^{3}} - { {\mathbf{OL}} \over OL^{3}} \right]\\ &\simeq& {{\cal G} m} \left[ { {\mathbf{PO}} \over {D}^{3}} + { {\mathbf{OL}} \over PL^{3}} - { {\mathbf{OL}} \over {D}^{3}} \right]\\ \end{eqnarray*}](../pages_maree-terrestre/equations_approche-statique/equation18.png)
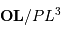 de l'équation précédente, en injectant la relation de Chasles
de l'équation précédente, en injectant la relation de Chasles 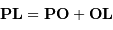 , et toujours au premier ordre en
, et toujours au premier ordre en 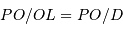 :
:
![\begin{eqnarray*} { {\mathbf{OL}} \over PL^{3}}&=& { {\mathbf{OL}} \over [{ {\mathbf{PL}}^{2}}]^{3/2}}= { {\mathbf{OL}} \over [( {\mathbf{PO}}+ {\mathbf{OL}})^{2}]^{3/2}}\\ \\ &\simeq& { {\mathbf{OL}} \over {D}^{3} \left( 1 + 2\ {\mathbf{PO}} . {\mathbf{OL}} / {D}^{2} \right)^{3/2}}\\ &\simeq& { {\mathbf{OL}} \over {D}^{3}} \left(1 - 3\ {\mathbf{PO}} . {\mathbf{OL}} / {D}^{2} \right)\\ \end{eqnarray*}](../pages_maree-terrestre/equations_approche-statique/equation22.png)
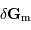 , en introduisant les
vecteurs unitaires
, en introduisant les
vecteurs unitaires 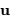 et
et 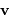 tels que
tels que 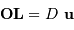 et
et 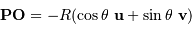 :
:
![\begin{eqnarray*} \delta \mathbf{G} _{\mathrm{m}} &=& {{\cal G} m} \left[ { {\mathbf{PO}} \over {D}^{3}} - {3\ {\mathbf{PO}} . {\mathbf{OL}} \over {D}^{2}}\ { {\mathbf{OL}} \over {D}^{3}} \right]\\ &=& {{\cal G} m\over {D}^{3}} \left[-R\ (\cos\theta\ \mathbf{u} + \sin\theta\ \mathbf{v}) + 3 R\ \cos\theta\ \mathbf{u} \right]\\ &=& {{\cal G} m R\over {D}^{3}} \left[2 \cos \theta\ \mathbf{u} - \sin \theta\ \mathbf{v} \right]\\ \end{eqnarray*}](../pages_maree-terrestre/equations_approche-statique/equation28.png)
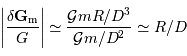
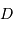 au corps provoquant la marée.
au corps provoquant la marée.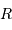 de l'objet affecté.
de l'objet affecté.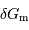 de la Lune sur la Terre de la
de la Lune sur la Terre de la 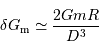
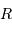 le rayon de la Terre,
le rayon de la Terre, 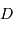 , la distance Terre-Lune (
, la distance Terre-Lune (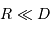 ), et
), et 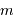 la masse de la Lune.
la masse de la Lune.
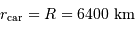 mesurant l'étendue d'eau, la hauteur
mesurant l'étendue d'eau, la hauteur 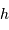 de la
marée est de l'ordre de 1 m.
de la
marée est de l'ordre de 1 m.
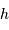 est, comme le champ de marée, une fonction
linéaire de
est, comme le champ de marée, une fonction
linéaire de 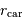 , estimer la hauteur de marée dans les cas suivants :
, estimer la hauteur de marée dans les cas suivants :
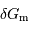 de la
Lune sur la Terre.
de la
Lune sur la Terre.
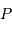 et
et 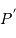 de la Terre, tels que
de la Terre, tels que 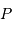 ,
, 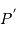 et
et 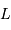 soient alignés, le point
soient alignés, le point 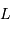 repérant le centre de la Lune.
Soit
repérant le centre de la Lune.
Soit 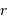 la distance
la distance 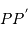 , et
, et 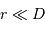 .
.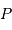 et
et 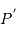 de façon à bien caractériser le problème.
de façon à bien caractériser le problème.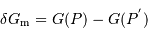 , en effectuant un développement limité au 1er ordre en
, en effectuant un développement limité au 1er ordre en 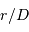 .
.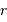 vaut
vaut 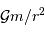 .
.
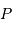 ou
ou 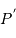 a intérêt à être confondu avec le centre de la Terre.
a intérêt à être confondu avec le centre de la Terre.
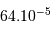
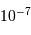
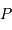 (centre de laTerre) :
(centre de laTerre) :
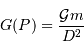
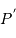 , côté opposé à la Lune. En ce point,
, côté opposé à la Lune. En ce point, 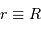 , et :
, et :
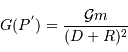
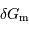 est alors:
est alors: