Sur l'orbite décrite par un corps autour d'une masse centrale, on va trouver des points d'équilibre utiles pour les satellites artificiels d'observation : les points de Lagrange.
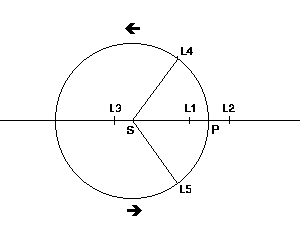
Pour obtenir une modélisation des mouvements dans le système solaire, on va partir du problème simplifié dans lequel les trajectoires des planètes sont des ellipses mais les éléments de ces ellipses vont varier au cours du temps. Cette ellipse de base est appelée ellipse osculatrice. Pour chaque planète on va considérer un problème à deux corps perturbé par les autres planètes. C'est Lagrange (1736-1813) au XVIIIème siècle qui a posé les équations du problème. Lagrange a aussi noté que dans un système à deux corps, il existait des positions d'équilibre où des corps supplémentaires pouvaient rester captifs. Ces positions sont appelées aujourd'hui les points de Lagrange du système à deux corps. La figure ci-dessous montrent l'emplacement des 5 points L1, L2, L3, L4, L5. Seuls les points L4 et L5 sont des points d'équilibre stables. Des astéroïdes sont piégés sur ces points de l'orbite de Jupiter et de celle de Mars. Les points L1 et L2 de la Terre permettent d'installer des télescopes d'observation (SOHO, un satellite d'observation du Soleil en L1 et bientôt GAIA, un satellite d'observation astrométrique de la galaxie en projet en L2). Les points L1 et L2 sont à 1,5 millions de kilomètres de la Terre.
Mécanique céleste, Temps et Calendriers
