Apprendre

Prérequis

Éléments de théorie cinétique du gaz parfait.

Gaz parfait

Rappel : un gaz est dit parfait si les interactions entre particules se réduisent à des chocs élastiques.

Pour un gaz parfait usuel, non dégénéré (c'est à dire non soumis à des effets quantique) et classique (c'est à dire non relativiste), l'équation d'état s'écrit :

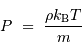
$P \ = \ {\rho k _{\mathrm{B}} T \over m}$

avec 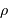$\rho$ la masse volumique, et 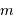la masse d'une particule élémentaire du gaz.

Un gaz parfait est dit chaud s'il est dominé par l'agitation thermique. Les effets quantiques sont dans ce cas négligeables.

Un gaz parfait est dit froid lorsque les effets thermiques ne jouent plus aucun rôle. Son incompressibilité provient du tassement de la matière : les cortèges électroniques se repoussent en raison de la nature quantique (fermionique) des électrons.

Température

Pour que la température d'un système soit définie, il faut que ce système soit à l'équilibre, et que ses composantes échangent assez d'informations, via des collisions, pour se thermaliser.

Dans un milieu non collisionnel, il y a peu de chances que l'on puisse définir une température qui vaille... mais on ne s'intéresse pas la suite qu'à des milieux à l'équilibre thermodynamique local, où localement la température est bien définie.

Densité particulaire

La densité particulaire est une grandeur couramment utilisée pour mesurer l'abondance de matériau disponible dans un milieu. Elle est comptée en particules (souvent des électrons, ou des atomes ou molécules d'hydrogène) par unité de volume. Par exemple : 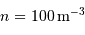$n = 100 \,\mathrm{m}^{-3}$ .

Énergie cinétique d'une particule

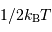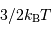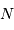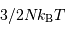L'énergie d'une particule vaut $1/2 k _{\mathrm{B}} T$ par degré de liberté. L'énergie cinétique de translation vaut $3/2 k _{\mathrm{B}} T$ . Pour une collection de particules, l'énergie cinétique totale se monte tout simplement à $3/2 N k _{\mathrm{B}} T$ .

Pression

Selon la théorie cinétique du gaz parfait, la pression, qui dimensionnellement est une densité d'énergie, correspond un flux de quantité de mouvement. En effet, l'énergie cinétique, fonction de la température, peut s'écrire en tenant compte de l'équation d'état du gaz parfait : 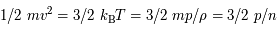$1/2\ mv^2 = 3/2\ k_{\mathrm{B}} T= 3/2\ mp / \rho = 3/2\ p/ n$ . avec 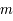la masse d'une particule et 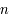la densité particulaire. 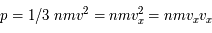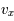On en déduit : $p = 1/3\ nmv^2 = nmv_x^2 = n m v_x v_x$ avec v_x la composante de la vitesse selon un seul axe (le milieu étant supposé homogène et isotrope : 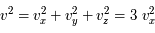$v^2 = v_x^2 + v_y^2 + v_z^2 = 3 \ v_x^2$ . 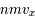On retrouve bien le flux de quantité de mouvement n m v_x .