Géostrophie

Auteurs: Thomas Navarro, Arianna Piccialli

Auteur: EM

Estimation de la circulation dans une dépression.

Difficulté : ☆☆ Temps : 30 min

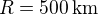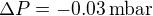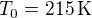On considère une dépression martienne de rayon $R = 500\,\mathrm{km}$ et de différence de pression en son centre avec la pression moyenne à la surface de Mars $\Delta P = -0.03\,\mathrm{mbar}$ . Cette dépression se situe à la latitude $\lambda = +45^\circ$ . On se placera par la suite dans le cadre de l'approximation géostrophique. 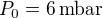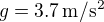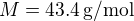La température moyenne sur Mars est voisine de $T_0 = 215\,\mathrm{K}$ , la pression moyenne de surface voisine de $P_0 = 6\,\mathrm{mbar}$ , l'accélération de la gravité y vaut $g=3.7\,\mathrm{m/s^2}$ et la masse molaire de l'atmosphère y est de $M = 43.4\,\mathrm{g/mol}$ .

Question 1)

Calculer la masse volumique 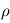$\rho$ de l'atmosphère à la surface de Mars.

Aide [1 points]

Question 2)

Calculer la valeur du paramètre de Coriolis 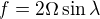$f = 2 \Omega \sin \lambda$ .

Aide [1 points]

Question 3)

Estimer l'ordre de grandeur du gradient radial de pression dans cette dépression.

Aide [1 points]

Question 4)

En appliquant la relation géostrophique, estimer la norme 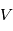de la vitesse du vent tangentiel à la distance 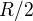R/2 du centre de la dépression. Quelle sera sa direction ?

Aide Aide [2 points]

Question 5)

Vérifier a posteriori la validité de l'approximation géostrophique.

Aide [1 points]

Question 6)

Les frottements à la surface entraînent une déviation du vent à proximité d'un angle valant 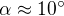$\alpha \approx 10^\circ$ par rapport aux isobares (considérés ici comme des cercles concentriques). Exprimer le flux de masse gazeuse entrant par la surface latérale de la dépression, de périmètre 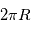$2\pi R$ et s'étendant verticalement sur une échelle de hauteur 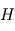. En déduire alors la vitesse moyenne verticale du vent au sein de la dépression et son signe (ascendant ou descendant).

Aide [2 points]