
|
Difficulté : ☆☆☆ Temps : 1 h
On modélise une tornade par une circulation tangentielle 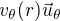 autour d'un centre. Le rayon caractéristique de la tornade est défini par
autour d'un centre. Le rayon caractéristique de la tornade est défini par 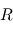 tel que : pour
tel que : pour 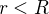 ,
, 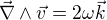 et pour
et pour 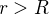 ,
, 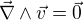 .
.
À l'aide du théorème de Stokes, donner l'expression de 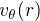 en tout point de l'espace. Exprimer en particulier la vitesse maximale
en tout point de l'espace. Exprimer en particulier la vitesse maximale 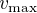 en fonction de
en fonction de 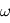 et de
et de 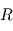 . Où est-elle atteinte ?
. Où est-elle atteinte ?
Aide [2 points]
En pratique, 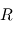 est inférieur au kilomètre et
est inférieur au kilomètre et 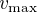 de l'ordre de 100 m/s. Quelle approximation est la plus justifiée : cyclostrophique ou géostrophique ?
de l'ordre de 100 m/s. Quelle approximation est la plus justifiée : cyclostrophique ou géostrophique ?
Exprimer alors une équation différentielle portant sur la pression 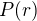 . On considèrera par la suite que
. On considèrera par la suite que 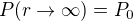 .
.
On considère la masse volumique 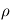 de l'atmosphère constante. Intégrer alors cette équation différentielle et exprimer
de l'atmosphère constante. Intégrer alors cette équation différentielle et exprimer 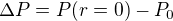 en fonction de
en fonction de 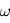 ,
, 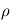 et
et 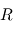 , puis de
, puis de 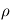 et
et 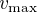 . Justifier le signe de
. Justifier le signe de 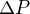 .
.
Aide [3 points]
Application numérique Exprimer 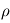 à la surface pour la Terre et pour Mars à l'aide de la loi des gaz parfaits. À l'aide des données du cours, calculer alors
à la surface pour la Terre et pour Mars à l'aide de la loi des gaz parfaits. À l'aide des données du cours, calculer alors 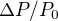 pour une tornade terrestre avec
pour une tornade terrestre avec 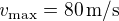 . En supposant la même valeur de
. En supposant la même valeur de 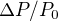 sur Mars, estimer alors
sur Mars, estimer alors 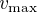 sur Mars.
sur Mars.
Aide [1 points]