Vent thermique géostrophique

Auteurs: Thomas Navarro, Arianna Piccialli

Auteur: EM

Courant jet sur Terre

Difficulté : ☆☆☆ Temps : 1 h

On considère les températures moyennées (zonalement, c'est-à-dire en longitude) au niveau de la surface pour les mois de janvier (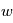) et juillet (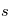) à différentes latitudes sur Terre.

Moyenne zonale des températures
Latitude	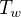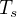[°C]	[°C]
30°N	+12	25
45°N	0	20
60°N	-12	15

Question 1)

Estimer le gradient de température sur la direction nord-sud à 45°N en janvier et en juillet. On donne le rayon terrestre 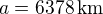$a = 6378\,\mathrm{km}$ .

Aide [2 points]

Question 2)

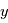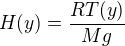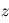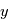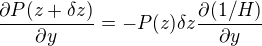
Difficile et facultatif Des différences horizontales de température (selon ici) se traduisent par des différences horizontales d'échelle de hauteur atmosphérique $H(y) = \frac{R T(y)}{Mg}$ . En supposant les pression au niveau uniformes selon , montrer que les pressions à l'altitude $\delta z \ll H$ sont telles que : $\frac{\partial P(z+\delta z)}{\partial y} = -P(z) \delta z \frac{\partial (1/H)}{\partial y}$

Aide Aide [2 points]

Question 3)

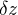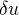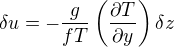Difficile et facultatif Le léger (d'ordre 1 en $\delta z$ ) gradient horizontal de pression ainsi créé engendre un léger vent géostrophique $\delta u$ . Montrer que $\delta u = - \frac{g}{fT} \left( \frac{\partial T}{\partial y} \right) \delta z$ .

Aide Aide [2 points]

Question 4)

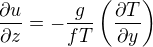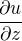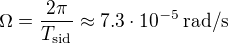L'équation obtenue précédemment se généralise sous la forme $\frac{\partial u}{\partial z} = -\frac{g}{fT} \left( \frac{\partial T}{\partial y} \right)$ et s'appelle équation du vent thermique. Calculer le cisaillement vertical du vent zonal $\frac{\partial u}{\partial z}$ en utilisant cette équation. On donne la vitesse angulaire de la rotation sidérale terrestre $\Omega = \frac{2 \pi}{T_{\mathrm{sid}}} \approx 7.3 \cdot 10^{-5} \,\mathrm{rad/s}$ .

Aide [1 points]

Question 5)

En considérant le vent nul à la surface et la température constante avec l'altitude, estimer alors la vitesse du vent zonal au sommet de la troposphère à une altitude 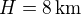$H = 8\,\mathrm{km}$ (soit environ une échelle de hauteur) en hiver puis en été. Dans quelle direction souffle ce vent (appelé courant jet) ?

Aide [2 points]