Ressources libres - Lumières sur l’Univers
Entrée du siteSommaireGlossairePage pour l'impression<-->
- Structure thermique des atmosphères planétaires
- Se tester
- Exercices
• Exercices courts
• Temps radiatif
• Étude d'une atmosphère fictionnelle

Étude d'une atmosphère fictionnelle

Auteur: EM
Auteur: Emmanuel Marcq
calcotron

exerciceExercice

Vous venez d'être embauché par un célèbre réalisateur Hollywoodien en tant que conseiller scientifique pour son prochain film de science-fiction. L'action se déroulera sur une lune tellurique nommée Pandore d'une planète géante appelée Polyphème en orbite autour de l'étoile 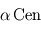\alpha\,\mathrm{Cen}. Toutes les données numériques pertinentes se trouvent ci-dessous.

Données numériques pertinentes

Étoile (α Centauri) :

  • Masse : 1,1 masse solaire
  • Rayon : 1,27 rayon solaire
  • Classe spectrale : G2V
  • Température photosphérique : 5790 K

Polyphème :

  • Masse : 0,44 masse jovienne
  • Rayon : 0,75 rayon jovien
  • Période de rotation : 15 h
  • Période de révolution : 1,4 année terrestre
  • Rayon de l'orbite : 1,32 UA
  • Albédo visible : 0.4

Pandore :

  • Rayon : 0,78 rayon terrestre
  • Masse : 0,43 masse terrestre
  • Rayon de l'orbite : 264000 km
  • Période de rotation (synchrone avec révolution) : 31,5 h
  • Albédo visible : 0,3
  • Pression atmosphérique à la surface : 1,22 bar
  • Température moyenne de surface : 27°C
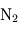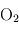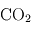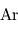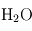  • Composition atmosphérique (% en masse) : \mathrm{N_2} (81 %), \mathrm{O_2} (16 %), \mathrm{CO_2} (2 %), \mathrm{Ar} (1 %), \mathrm{H_2O} (variable), 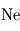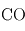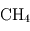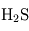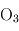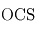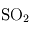\mathrm{Ne}, \mathrm{CO}, \mathrm{CH_4}, \mathrm{H_2S}, \mathrm{O_3}, \mathrm{OCS}, \mathrm{SO_2} (traces).
  • Capacité calorifique à pression constante : 1012 J/kg/K
Question 1)
  1. Quelle est la puissance lumineuse totale émise par l'étoile hôte ?
  2. Calculer alors la constante stellaire au niveau de l'orbite de Polyphème.

AideSolution

Question 2)
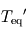  1. Calculer la température d'équilibre {T_{\mathrm{eq}}}' de la planète géante
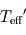  2. La température effective {T_{\mathrm{eff}}}' de Polyphème sera-t-elle supérieure ou inférieure à 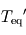{T_{\mathrm{eq}}}' ? Justifier.
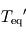  3. Bonus : proposer une composition possible des nuages visibles de Polyphème, situés à une altitude où la température est voisine de {T_{\mathrm{eq}}}'.

AideSolution

Question 3)
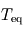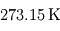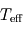  1. Calculer la température d'équilibre T_{\mathrm{eq}} de Pandore. La comparer à celle du point triple de l'eau, égale à 273.15\,\mathrm{K}. Que vaut alors T_{\mathrm{eff}} ?
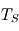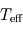  2. Quel est le nom du phénomène responsable de l'écart entre la température de surface T_S et T_{\mathrm{eff}} ? En donner une explication qualitative.

AideSolution

Question 4)

On se propose à présent d'estimer l'opacité infrarouge de l'atmosphère de Pandore à l'aide d'un modèle simple. L'atmosphère est supposée parfaitement transparente en lumière visible et absorbe la totalité des rayonnements infrarouges thermiques. La température de l'atmosphère, supposée uniforme, sera notée 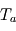T_a.

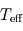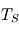  1. Faire un schéma en représentant de façon distincte les flux visible et IR thermique montants et descendants
  2. Exprimer le flux thermique s'échappant vers l'espace en fonction notamment de T_{\mathrm{eff}}.
  3. Effectuer un bilan des flux au niveau de la surface.
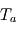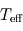  4. En déduire alors les expressions de T_S et T_a en fonction de T_{\mathrm{eff}}.
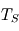  5. Effectuer l'application numérique et comparer avec la valeur de T_S donnée dans l'énoncé. Que constate-t-on ? Proposer une explication.

AideSolution

Question 5)

Afin d'améliorer ce modèle, on ajoute une seconde couche atmosphérique partiellement opaque aux IR thermiques au-dessus de la première couche (qui reste complètement opaque à ces mêmes IR thermiques). On note la température de la couche supérieure 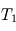T_1 et celle de la couche profonde 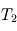T_2. La couche 1 absorbe une fraction 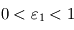0 < \varepsilon_1 < 1 du rayonnement IR thermique. Ces deux couches sont toujours considérées parfaitement transparentes en lumière visible.

  1. Faire un nouveau schéma représentant les différents flux.
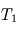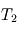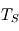  2. En effectuant trois bilans respectivement au niveau de l'espace, de la couche semi-transparente aux IR et à la surface, déterminer un système de trois équations à trois inconnues T_1, T_2 et T_S. On fera apparaître l'expression de 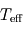T_{\mathrm{eff}} dans ce système.
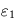  3. Résoudre ce système d'équations. En déduire la valeur de \varepsilon_1, puis celles de 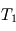T_1 et T_2.
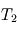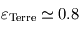  4. Sur Terre, une modélisation analogue ne nécessite qu'une seule couche semi-transparente aux IR sans couche profonde (\varepsilon_{\mathrm{Terre}} \simeq 0.8). Comparer l'intensité de l'effet de serre sur Terre et sur Pandore.

AideSolution

Question 6)

Compte tenu de la composition atmosphérique, s'attend-on à trouver une stratosphère sur Pandore ? Si oui, quelle serait l'espèce chimique responsable ?

AideSolution

Question 7)
  1. Calculer la masse molaire moyenne de l'atmosphère ainsi que la gravité de surface.
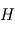  2. En déduire l'échelle de hauteur atmosphérique H au niveau de la surface.
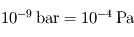  3. La limite de l'atmosphère (exobase) se situe à une pression de 10^{-9}\,\mathrm{bar} = 10^{-4}\,\mathrm{Pa}. Estimer l'altitude de cette exobase (on considérera 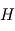H constant pour ce calcul).

AideSolution

Question 8)

Calculer le gradient adiabatique sec 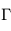\Gamma. Le gradient adiabatique humide sera-t-il inférieur ou supérieur en valeur absolue ?

AideSolution

Question 9)

Représenter l'allure du profil thermique moyen de Pandore. On considérera que la troposphère s'étend sur une échelle de hauteur H, et on fera figurer l'échelle de hauteur, les différentes couches atmosphériques et les températures à leurs limites quand cela est possible.

AideSolution

Page précédentePage suivante