
|
Difficulté : ☆☆☆ Temps : 45 min
On considère une atmosphère transparente en lumière visible et partiellement opaque aux IR thermiques (absorbance et émissivité 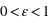 ), et de température uniforme
), et de température uniforme 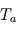 à l'équilbre radiatif. À l'instant intial, on perturbe la température de cette atmosphère d'une quantité
à l'équilbre radiatif. À l'instant intial, on perturbe la température de cette atmosphère d'une quantité 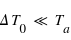 .
. 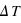 varie ensuite en fonction du temps.
varie ensuite en fonction du temps.
Pourquoi peut considérér que l'absorbance et l'émissivité de l'atmosphère sont égales (pour une longueur d'onde donnée) ?
Aide [1 points]
Exprimer le surcroît de flux thermique 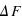 émis par une colonne atmosphérique de surface
émis par une colonne atmosphérique de surface 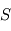 dans tout l'espace. On se limitera à l'ordre 1 en
dans tout l'espace. On se limitera à l'ordre 1 en 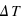 .
.
Exprimer la capacité calorifique (à pression constante)  de cette colonne d'atmosphère en fonction notamment de la capacité calorifique massique
de cette colonne d'atmosphère en fonction notamment de la capacité calorifique massique 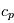 , de la pression de surface
, de la pression de surface 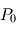 et de la gravité de surface
et de la gravité de surface 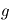 .
.
Aide [1 points]
Montrer alors que 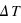 obéit à l'équation différentielle suivante :
obéit à l'équation différentielle suivante : 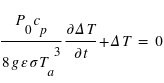
Aide [2 points]
Résoudre alors cette équation en faisant apparaître une constante de temps appelée temps radiatif 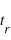 .
.
Aide [1 points]
Application numérique : on donne pour la Terre et pour Mars les valeurs suivantes.
| Terre | Mars | |
|---|---|---|
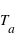 [K] [K] | 242 | 181 |
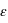 | 0,77 | 0,18 |
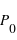 [Pa] [Pa] | 105 | 640 |
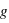 [m/s²] [m/s²] | 9,8 | 3,7 |
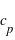 [J/K/kg] [J/K/kg] | 1000 | 800 |
Calculer 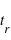 pour ces deux planètes.
pour ces deux planètes.
[1 points]
Estimer alors l'amplitude thermique diurne de température sur Terre et sur Mars.
Aide [2 points]