Coriolis et Lagrange
Coriolis et Lagrange
Difficulté : ☆☆
Temps : 45 min
Question 1)
Représenter l'allure du potentiel gravitationnel local autour de L4 dans le référentiel tournant avec les 2 corps, sachant qu'il y présente un maximum.
AideSolution
Tracer une coupe selon une direction, puis l'autre, sachant que L4 est un sommet
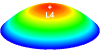
Le potentiel est d'allure parabolique. L4 est un maximum.
L'allure de la courbe de potentiel est :
Question 2)
Montrer que toute composante de vitesse s'éloignant radialement de L4 donne un terme de Coriolis conduisant à un mouvement de rotation autour de L4.
AideSolution
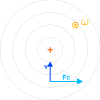
Munir le plan orbital d'un repère cartésien s'appuyant sur L4, et donner la direction du vecteur rotation par rapport à ce plan
La composante de Coriolis s'écrit 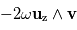 .
.
Etant perpendiculaire à la rotation, elle est nécessairement dans le plan orbital. Etant également perpendiculaire au mouvement, supposé radial, elle est nécessairement orthoradiale : elle va induire un mouvement de rotation autour de L4.
Question 3)
Montrer que toute composante de vitesse orthoradiale autour de L4 conduit à un terme de Coriolis radial. Déterminer le seul sens de rotation possible pour une orbite stable.
AideSolution
Il est nécessaire que cette composante de vitesse, radiale, soit de plus dirigée vers L4.
La composante de Coriolis s'écrit 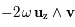 .
.
Toujours perpendiculaire à la rotation, elle reste nécessairement dans le plan orbital. Etant également perpendiculaire au mouvement, supposé orthoradial, elle est nécessairement radiale.
Afin que cette composante radiale agisse telle une force de rappel vers L4, un seul sens de rotation est possible : vérifier qu'il s'agit d'une rotation dans le même sens que la rotation orbitale.