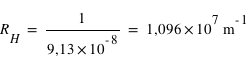Niveaux d'énergie de l'atome d'hydrogène
Niveaux d'énergie de l'atome d'hydrogène
Difficulté : ☆
Temps : 10 minutes
Question 1)
Calculer les énergies (en eV) des quatre premiers niveaux de l'atome d'hydrogène et donner le diagramme des niveaux d'énergie.
AideSolution
Il suffit d'utiliser la relation :
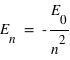
où E0=13,6 eV
Pour le premier niveau n=1 d'où 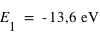 .
.
Pour le deuxième niveau n=2 d'où 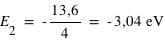
Pour le troisième niveau n=3 d'où 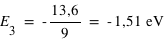
Pour le quatrième niveau on a n=4 d'où 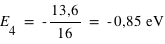
Le diagramme des niveaux d'énergie est le suivant:
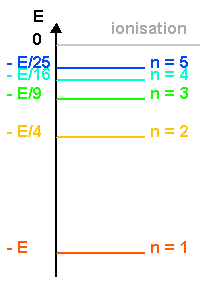
Crédit :
ASM

 Constante de Rydberg
Constante de Rydberg
Difficulté : ☆☆
Temps : 15 minutes
Question 1)
Connaissant l'énergie d'ionisation E0=13,6eV, calculer la valeur de RH dans l'expression :
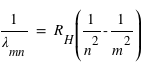
AideSolution
- Cherchons d'abord la valeur de la longueur d'onde associée à cette énergie :
Comme E=hν avec v = c/λ, d'où λ= hc/E0. Or on doit exprimer E0 en Joule. Comme 1eV=1,6.10-19J, alors
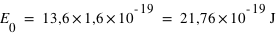 .
On en déduit alors la valeur : λ=9,13.10-8m.
.
On en déduit alors la valeur : λ=9,13.10-8m. - Quelles sont alors les valeurs de n et m?
Il s'agit d'une énergie d'ionisation donc m=∞ et n=1.
- On en déduit finalement la valeur de RH=1/ λ, puisque m=∞ et n=1.