Le premier système d'étoiles binaires spectroscopique fut découvert en 1889 par Antonia C. Maury, qui remarqua un dédoublement des raies dans le spectre de l'étoile 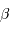 Aurigae. Les positions de ces raies, en longueur d'onde, varient au cours du temps, témoins de la variation de la vitesse radiale de chaque composante, par suite de leur mouvement orbital relatif.
Aurigae. Les positions de ces raies, en longueur d'onde, varient au cours du temps, témoins de la variation de la vitesse radiale de chaque composante, par suite de leur mouvement orbital relatif.
Les étoiles doubles spectroscopiques sont très nombreuses : on estime qu'en moyenne une étoile sur trois ou quatre est une double spectroscopique. Leurs périodes observées s'échelonnent entre quelques heures et quelques années. A partir de l'étude de la courbe de vitesse radiale, on peut calculer les paramètres définissant l'orbite elliptique d'une étoile par rapport à l'autre. Cette détermination se fait toutefois à l'effet de projection près, car on ne connaît pas a priori l'orientation du plan orbital dans l'espace. Actuellement, on connaît précisément les paramètres orbitaux pour environ un millier de ces objets.
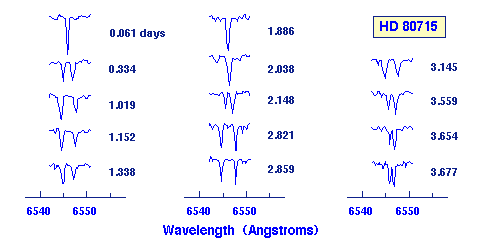
Dédoublement de raies de l'étoile
HD 80715
Crédit :
ASM
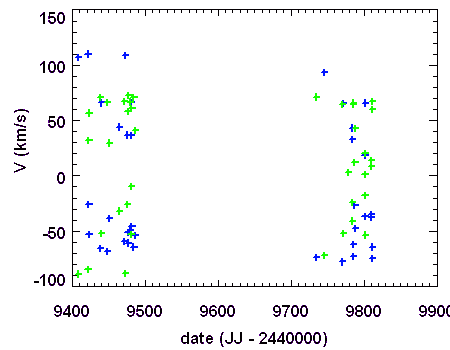
Série temporelle : mesure des vitesses radiales des 2 composantes de l'étoile 55 Uma
Crédit :
ASM
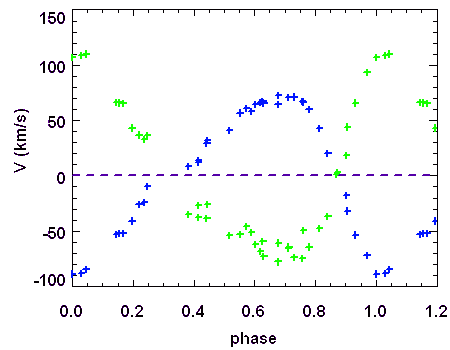
Courbe de vitesses radiales des 2 composantes de l'étoile double 55 Uma
Crédit :
ASM
Paramètres du mouvement
On peut ainsi représenter la variation de la vitesse des deux composantes (ou d'une seule, si une seule est détectable) en fonction du temps. Selon la forme de l'orbite et son orientation dans l'espace, les caractéristiques de la courbe de vitesse radiale observée seront différentes. L'analyse de cette courbe permet de remonter aux paramètres du mouvement et aux masses des composantes.
Masses
Par définition du centre de masse : 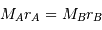 . On obtient alors le rapport des masses :
. On obtient alors le rapport des masses :
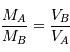
qui est donné par le rapport des amplitudes des deux courbes. D'autre part, d'après la troisième loi de Kepler, on a :
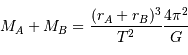
On obtient :
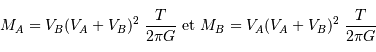
Si l'inclinaison  est différente de
est différente de 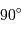 , l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur
, l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur 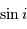
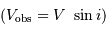 .
.
Dans les équations précédentes, 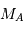 est donc remplacé par
est donc remplacé par 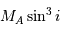 (respectivement
(respectivement 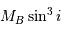 ).
).
Orbite elliptique
Si l'orbite n'est pas circulaire mais elliptique avec une excentricité 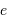 non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
 Observabilité
Observabilité
Difficulté : ☆
Temps : 5 min
Question 1)
Comment se révèle à l'observation une étoile double spectroscopique dans le cas où 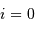 ?
?
 Résolution spectrale
Résolution spectrale
Difficulté : ☆☆
Temps : 20 min
On cherche à analyse un spectre d'étoile spectroscopique double, enregistré avec une résolution dans le domaine visible 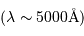 de l'ordre de
de l'ordre de 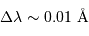 .
.
Question 1)
Quelle limitation cela impose-t-il sur les vitesses radiales que l'on peut effectivement mesurer ?
Voir le cours sur l'effet Doppler issues de mesures spectrométriques.
Question 2)
Observer des grandes vitesses orbitales favorise-t-il ou non les systèmes serrés ?
 Inclinaison de l'orbite
Inclinaison de l'orbite
Difficulté : ☆
Temps : 10 min
Question 1)
Comment peut-on vérifier que l'hypothèse 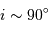 est vraie ou non ?
est vraie ou non ?
Question 2)
Quand l'inclinaison est inconnue, peut-on obtenir des limites inférieures ou supérieures pour les masses des deux composantes ?
 L'étoile double AR Lacertae
L'étoile double AR Lacertae
Difficulté : ☆
Temps : 30 min
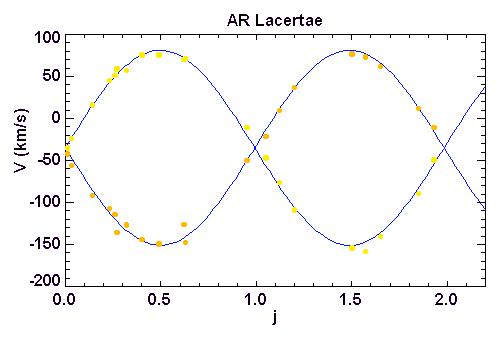
Courbe de vitesse radiale de AR Lacertae
Crédit :
ASM
On considère l'étoile double AR Lacertae, dont on a observé les courbes des vitesses radiales des deux composantes. La période du système vaut 1.983 j.
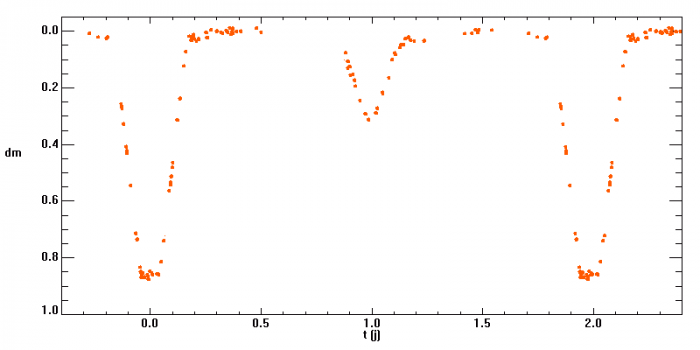
Courbe de lumière de AR Lacertae
Crédit :
ASM
Question 1)
Commenter les courbes. Que dire des caractéristiques du mouvement des deux étoiles ?
[1 points]
Question 2)
Quelle est la vitesse radiale du barycentre ?
[1 points]
Question 3)
Trouver le rapport des masses des deux composantes.
[1 points]
Question 4)
Trouver la séparation (en km) des deux composantes.
[1 points]
Question 5)
Déterminer la masse de chaque composante en unité solaire
[1 points]
Question 6)
Dans quel cas serait-il possible de calculer les rayons de chaque étoile ?
[1 points]
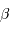 Aurigae. Les positions de ces raies, en longueur d'onde, varient au cours du temps, témoins de la variation de la vitesse radiale de chaque composante, par suite de leur mouvement orbital relatif.
Aurigae. Les positions de ces raies, en longueur d'onde, varient au cours du temps, témoins de la variation de la vitesse radiale de chaque composante, par suite de leur mouvement orbital relatif.



 de l'orbite sur le ciel n'est pas nulle, produit des variations périodiques de la vitesse radiale (vitesse projetée le long de la ligne de visée) des deux étoiles par rapport à l'observateur. L'effet
de l'orbite sur le ciel n'est pas nulle, produit des variations périodiques de la vitesse radiale (vitesse projetée le long de la ligne de visée) des deux étoiles par rapport à l'observateur. L'effet 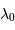 observée des raies émises à
observée des raies émises à 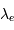 par le couple d'étoiles.
par le couple d'étoiles.
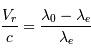
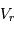 est la vitesse radiale d'une des composantes et
est la vitesse radiale d'une des composantes et 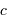 est la vitesse de la lumière.
est la vitesse de la lumière.

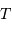 est un peu inférieure à 3 jours.
est un peu inférieure à 3 jours.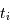 , estimer une phase du type
, estimer une phase du type 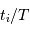 .
.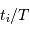 (fonction
(fonction 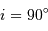 (le plan de l'orbite contient la ligne de visée). Les deux courbes de vitesse radiale sont alors des sinusoïdes qui oscillent en opposition de phase, autour de la vitesse
(le plan de l'orbite contient la ligne de visée). Les deux courbes de vitesse radiale sont alors des sinusoïdes qui oscillent en opposition de phase, autour de la vitesse 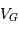 de leur barycentre, avec une même période
de leur barycentre, avec une même période 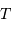 .
.
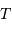 autour de G, les vitesses
autour de G, les vitesses 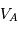 et
et 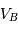 sont liées aux distances
sont liées aux distances 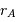 et
et 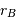 par les relations :
par les relations :
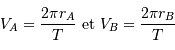
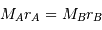 . On obtient alors le rapport des masses :
. On obtient alors le rapport des masses :
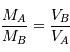
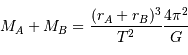
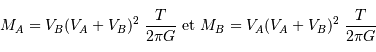
 est différente de
est différente de 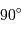 , l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur
, l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur 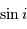
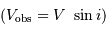 .
.
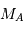 est donc remplacé par
est donc remplacé par 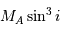 (respectivement
(respectivement 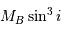 ).
).
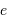 non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
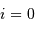 ?
?
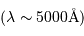 de l'ordre de
de l'ordre de 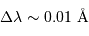 .
.
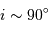 est vraie ou non ?
est vraie ou non ?


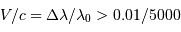
 .
.
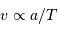 au demi-grand axe s'exprime :
au demi-grand axe s'exprime :
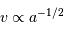
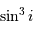 , on obtient bien une limite inférieure pour la masse de chaque composante.
, on obtient bien une limite inférieure pour la masse de chaque composante.