Se repérer, dans le temps comme dans l'espace, est à la base de toute bonne astrophysique.
Il suffit, pour s'en convaincre, de penser à l'étape première de l'analyse d'un problème mécanique : la nécessaire identification d'un référentiel, càd d'un solide sur lequel appuyer l'étude, muni d'une horloge fiable et précise. Pour permettre des mesures, ce référentiel doit s'accompagner d'un repère.
Ce chapitre aborde ainsi les mesures de temps et d'espace qui serviront de cadre de travail à tout le cours.
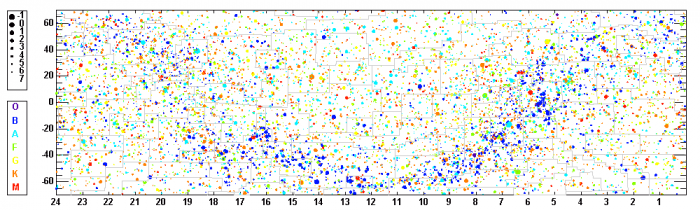
Carte du ciel (ascension droite en abscisse, déclinaison en ordonnée), avec toutes les étoiles de
magnitude plus brillante que 6. La taille du symbole est proportionnelle à la
magnitude, et la couleur représente
le type spectral . La région la plus riche en étoiles est notre Galaxie, vue par la tranche.
Crédit :
BSC/ASM
Du bon usage des distances
Lorsque l'on parcourt la littérature astrophysique, les longueurs ou distance apparaissent souvent exprimées dans des unités inhabituelles.
Les distances sont couramment rapportées :
- en distance angulaire sur le ciel ; la conversion en distance linéaire nécessite de connaître l'éloignement à l'objet.
- en temps de lumière.
- en parsec, ou en multiple du parsec ; ce qui nécessite une définition.
- en décalage spectral
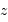 ; ce qui nécessite une interprétation.
; ce qui nécessite une interprétation.
Mètre étalon

Un des nombreux mètres étalons installés sur la voie publique, pour aider à l'usage de cette nouvelle unité, définie dans l'enthousiasme révolutionnaire.
Crédit :
ASM
France
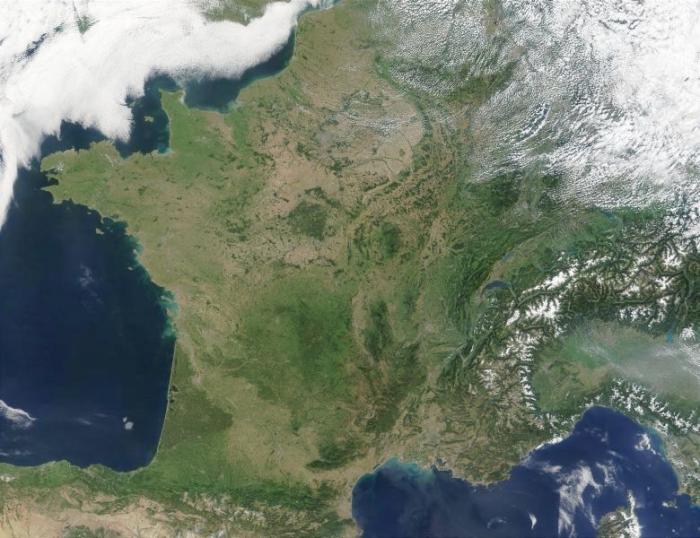
La France vue du ciel.
Crédit :
NASA
L'étoile Bételgeuse

Seules les étoiles les plus grosses, et proches, laissent entrevoir leur
diamètre physique. Sinon, on ne peut en apercevoir que la tache de diffraction (image de droite).
Crédit :
HST
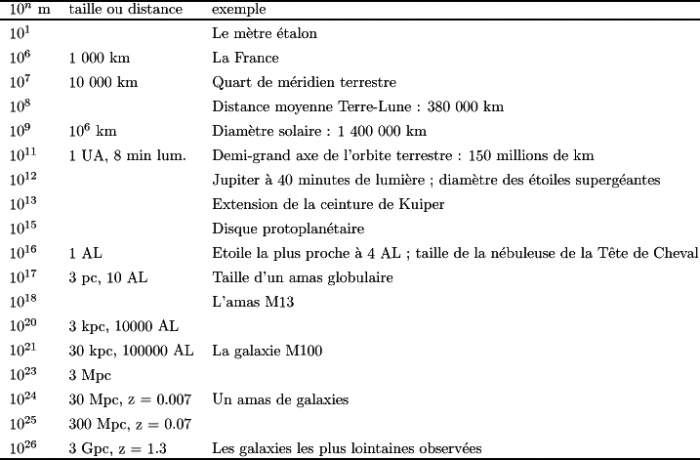
Par pas de 10
Crédit :
ASM
La nébuleuse de la Tête de Cheval dans Orion

Cette nébuleuse, trop faible pour apparaître sur une observation non posée, correspond à une partie d'un nuage interstellaire froid, qui absorbe la lumière des sources en arrière plan et se découpe en ombre chinoise sur le fond lumineux.
Crédit :
CFHT
Messier 13

Amas globulaire M13, réunissant de l'ordre de 300 000 étoiles, liées gravitationnellement. Son diamètre est estimé à 130 AL.
Crédit :
OHP/CNRS
Messier 100

Galaxie spirale vue de face. Son diamètre est de l'ordre de 100 000 AL.
Crédit :
CFHT
Un amas de galaxies

Crédit :
HST
Par pas de 10
La liste ci-jointe et le tableau ci-dessous proposent une promenade dans les distances et longueurs, par pas de 10, pour passer du mètre à l'échelle la plus vaste que l'on puisse imaginer dans l'Univers.
 Objectifs
Objectifs
Comme le parcours de l'échelle du mètre à celle de l'Univers s'étend sur 26
ordres de grandeurs,
il apparaît rapidement que le mètre est une unité malcommode pour
estimer la plupart des longueurs et distances rencontrées. D'où la
nécessité d'introduire des unités appropriées,
qui permettent d'exprimer les distances avec des nombres
plutôt voisins de l'unité que de milliards de milliards de mètres.
Le temps de lumière
Le temps de lumière permet d'estimer les distances, qu'elles soient
courtes (la Terre est à 8 minutes de lumière du Soleil), ou longues (les
galaxies les plus lointaines observées sont à environ 12 milliards
d'années de lumière).
L'unité astronomique
Dans le système solaire, ou pour des dimensions dans un environnement
stellaire, on s'appuie sur le demi-grand axe de l'orbite de la Terre, et
on utilise couramment l'unité astronomique (UA).
 Définition
Définition
Par
définition, il s'agit du demi-grand axe de l'orbite terrestre, soit environ 150 millions de km (plus précisément : 149 597 870 km)
La parallaxe
Le mouvement de la Terre autour du soleil se traduit par un mouvement apparent des étoiles du proche voisinage solaire, qui semblent parcourir une petite ellipse sur le fond des étoiles plus lointaines, fixes.
 Définition
Définition
La parallaxe annuelle 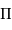 mesure le demi-grand axe angulaire de ce mouvement apparent.
mesure le demi-grand axe angulaire de ce mouvement apparent.
Les parallaxes sont usuellement exprimées en millièmes de seconde d'arc (mas).
L'étoile la plus proche, Proxima du Centaure, a une parallaxe de 772 mas.
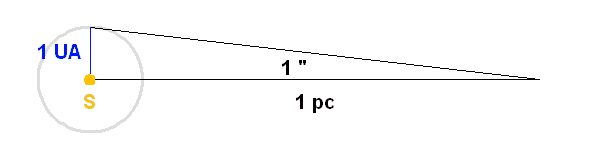
1 pc est la distance sous laquelle 1 UA sous-tend 1". Cette définition provient bien sûr du mouvement de parallaxe annuelle des étoiles proches.
Crédit :
ASM
Le parsec
Une unité propre à l'astrophysique est le parsec, noté pc.
 Définition
Définition
Le parsec est la distance à laquelle 1 unité astronomique sous-tend 1 seconde d'arc.
On emploie couramment les unités multiples du parsec : kpc, Mpc, Gpc.
Cette définition du parsec est opérationnelle : elle est reliée
au mouvement de parallaxe annuelle des étoiles proches.
En application directe de la définition, un objet de taille angulaire 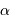 exprimée en seconde d'arc vu à une distance
exprimée en seconde d'arc vu à une distance 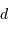 exprimée en parsec possède une taille linéaire
exprimée en parsec possède une taille linéaire 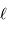 , exprimée en unité astronomique (dans l'approximation des petits angles) :
, exprimée en unité astronomique (dans l'approximation des petits angles) :
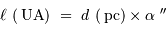
La parallaxe
Plus une étoile est éloignée, moins sa parallaxe est marquée.
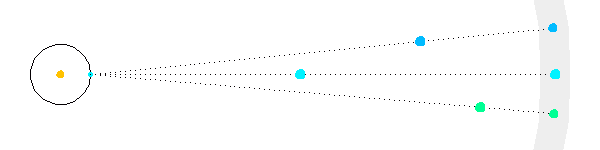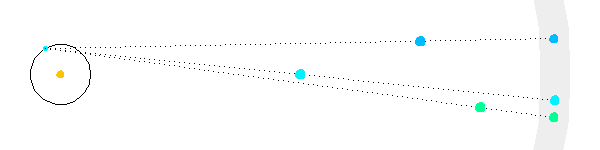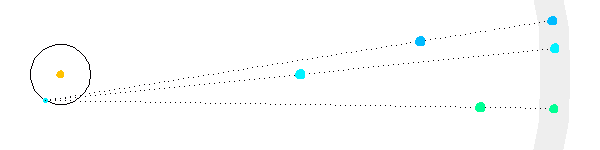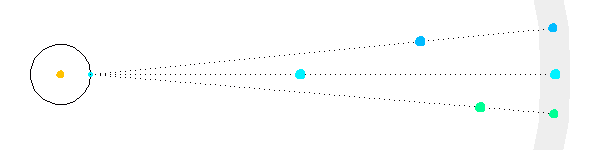
La rotation de la Terre autour du Soleil se traduit par un mouvement d'oscillation des étoiles proches sur le fond du ciel (modélisé en gris), d'amplitude décroissant avec la distance.
Crédit :
ASM
Mouvement apparent parallactique
Le mouvement apparent parallactique, créé par la rotation de la Terre autour du Soleil, dépend de la position de l'étoile par rapport à l'écliptique.
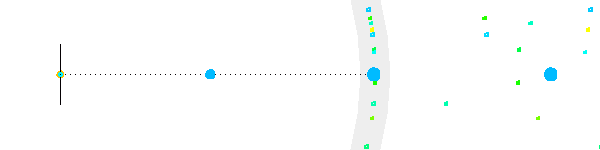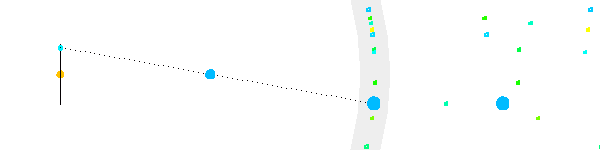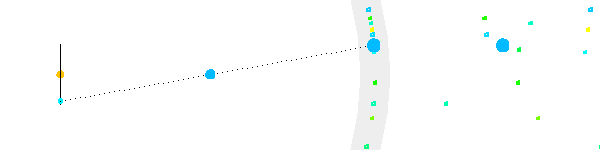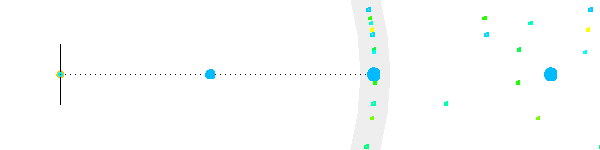
Le mouvement parallactique d'une étoile proche d'un pôle céleste est quasiment circulaire.
Crédit :
ASM
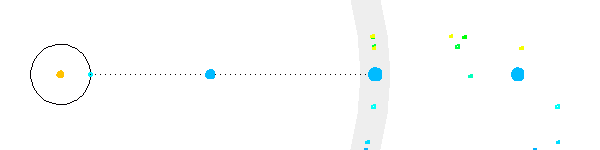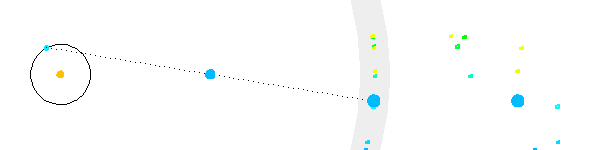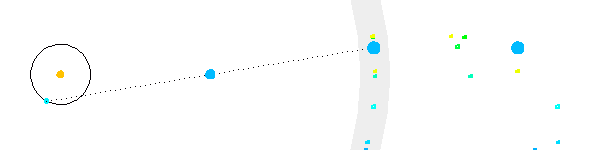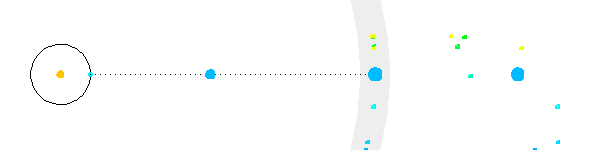
Le mouvement parallactique d'une étoile proche de l'équateur céleste est quasiment rectiligne.
Crédit :
ASM
 Une pomme et des pépins
Une pomme et des pépins
Difficulté : ☆
Temps : 15 min
Un peu d'exercice sur les ordres de grandeurs.
Données
| Rayon du Soleil | 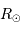 | 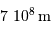 |
| Rayon de la Terre | 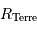 | 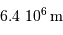 |
| Diamètre d'une pomme | 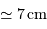 | |
Question 1)
La taille du Soleil étant rapportée à celle d'une pomme, quelle est à
cette échelle la taille de la Terre ?
Question 2)
A quelle distance se situe la pomme la plus proche, l'étoile Proxima du Centaure éloignée de 1,31 pc du Soleil.
 Le groupe local
Le groupe local
Difficulté : ☆
Temps : 20 min
Question 1)
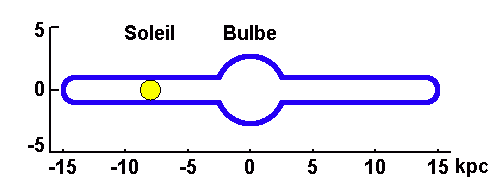
Faire un schéma de la Galaxie vue par la tranche.
Echelle conseillée : 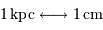
Question 2)
Faire un schéma de notre Galaxie dans le groupe local, comprenant entre autres la galaxie d'Andromède,
située à 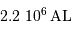 et de taille comparable à notre galaxie, et le Grand Nuage de Magellan,
situé à
et de taille comparable à notre galaxie, et le Grand Nuage de Magellan,
situé à 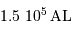 et de diamètre
et de diamètre 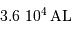 . Respecter une même échelle pour les tailles et distances.
. Respecter une même échelle pour les tailles et distances.
Echelle conseillée : 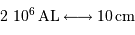
 L'Univers est plein de vide
L'Univers est plein de vide
Difficulté : ☆☆
Temps : 30 min
Le bulbe galactique présente une densité moyenne de 3 étoiles par 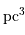 . On suppose que ces étoiles sont toutes de même type, de rayons
. On suppose que ces étoiles sont toutes de même type, de rayons 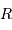 identiques.
identiques.
Données
| Diamètre du bulbe | 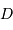 | 5.4 kpc |
| Rayon stellaire moyen | 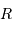 | 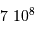 m m |
| Diamètre du vaisseau | 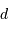 | 1 km |
Question 1)
Estimer la probabilité de collision entre une étoile et un vaisseau intergalactique de
rayon 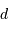 traversant le bulbe de part en part.
traversant le bulbe de part en part.
Déterminer le volume balayé par le vaisseau, nécessaire pour traverser la galaxie de part en part sans "toucher" une seule étoile.
Ce volume est cylindrique ; son rayon dépend surtout de la taille des étoiles, pas de celle du véhicule, car il est très petit par rapport à une étoile.
Comparer le volume précédemment trouvé au volume moyen offert à une étoile.
Question 2)
Etes-vous partant pour piloter le vaisseau ? Pourquoi le bulbe d'une galaxie présente-t-il cet
aspect si dense?
M31

Crédit :
CFHT
Bien répertorier les conditions du voyage : risque de collisions, durée du trajet, pause sandwich...
Que voit-on exactement d'une étoile : un point, un disque, une tache de diffraction ? Et combien d'étoiles a-t-on sur un pixel ?
 Le laser-lune
Le laser-lune
Difficulté : ☆
Temps : 20 min

Le télescope laser-lune du CERGA, à Grasse.
Crédit :
OCA/CERGA
Un télescope laser-lune mesure la distance Terre-Lune par la mesure du trajet aller-retour d'un faisceau laser envoyé par le télescope, réfléchi par des rétro-réflecteurs (déposés sur la Lune par des missions américaines et des sondes soviétiques), et reçu par le télescope.
Question 1)
Rétro-réflecteur
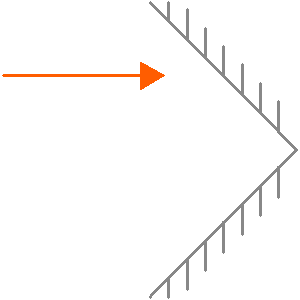
Rétro-réflecteur.
Crédit :
ASM
Le principe des rétroréflecteurs correspond au schéma ci-joint.
Expliquer le fonctionnement en illustrant le trajet des rayons lumineux
sur ce schéma. On étudiera le cas de plusieurs angles incidents différents.
Quelle est la propriété du faisceau réfléchi ? Est-elle utile ?
[1 points]
Question 2)
La distance Terre-Lune valant en moyenne 380 000 km, déterminer la durée du trajet du faisceau lumineux. La précision temporelle de la mesure étant de l'ordre de quelques dizaines de picosecondes, en déduire l'ordre de grandeur de
la précision en distance par le faisceau laser.
[1 points]
 Lentille gravitationnelle
Lentille gravitationnelle
Difficulté : ☆☆
Temps : 40 min
On souhaite mesurer le décalage temporel entre 2 images d'une même source, résultant du phénomène de lentille gravitationnelle : la lumière d'une source lointaine (typiquement un quasar) est défléchie par la présence d'une masse élevée (typiquement un amas de galaxies) sur la ligne de visée. Cette déflexion s'interprète dans le cadre de la relativité générale : la présence d'une très grande masse courbe l'espace-temps, ce qui infléchit la trajectoire de la lumière. On suppose la géométrie de l'observation fixée par le schéma ci-joint, avec 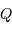 le quasar et
le quasar et 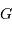 l'amas de galaxies et T la Terre.
l'amas de galaxies et T la Terre.
Lentille gravitationnelle

Phénomène de lentille gravitationnelle observé par le télescope spatial HST en direction de l'amas Abell 1689. De multiples images d'un quasar sont visibles, qui apparaissent comme des arcs centrés sur l'amas déflecteur.
Crédit :
NASA
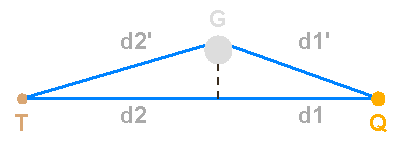
Schématisation de l'effet de lentille gravitationnelle.
Crédit :
ASM
Question 1)
Déterminer la distance 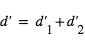 correspondant au trajet dévié quasar-lentille-Terre. On note
correspondant au trajet dévié quasar-lentille-Terre. On note 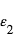 le petit angle entre l'image directe et l'image déviée.
le petit angle entre l'image directe et l'image déviée.
[2 points]
Travailler dans l'approximation des petits angles.
Si 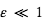 ,
, 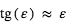 et
et 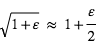
Question 2)
Expliciter la différence de chemin optique entre les 2 rayons.
[1 points]
Question 3)
Faire l'application numérique. On prendra 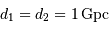 et
et 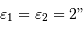 . Donner le résultat en pc ainsi qu'en temps de lumière.
. Donner le résultat en pc ainsi qu'en temps de lumière.
[2 points]
Question 4)
Certains quasars présentent des variations rapides de flux et sont vus sous différents angles, suite à de multiples chemins optiques possibles, plus ou moins déviés selon la géométrie (potentiellement complexe) du déflecteur.
Estimer l'ordre de grandeur du délai maximal entre 2 images du quasar ?
[1 points]
 Globules déphasés
Globules déphasés
Difficulté : ☆☆
Temps : 1 h
Dans cet exercice, l'étoile céphéide RS Pup éclaire des globules de son environnement. On détecte la courbe de lumière de l'étoile. Les globules montrent une courbe de lumière avec les mêmes variations mais décalées d'un temps qui correspond au temps mis par la lumière pour aller de l'étoile au globule. Le but de l'exercice est d'estimer quel déphasage est attendu pour chaque globule.
Pour cela, on se propose d'abord, à l'aide de l'appliquette ci-jointe, d'estimer la distance angulaire entre la céphéide RS Pup et les globules de la nébuleuse de son environnement. On suppose que les globules et l'étoile sont dans le même plan.
RS Pup 

Question 1)
À partir de l'échelle, étalonner le rapport d'unité u, pour retranscrire directement une mesure non pas en pixel mais en seconde d'arc.
[1 points]
Se servir de la fonction ligne.
Question 2)
Estimer la distance angulaire 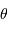 de chaque globule et remplir la colonne correspondante du tableau présenté par la 2ème appliquette.
de chaque globule et remplir la colonne correspondante du tableau présenté par la 2ème appliquette.
[1 points]
Avoir 3 onglets ouverts, pour le cours et chacune des appliquettes.
Sélectionner la case à remplir, et rentrer sa valeur précédée d'un symbole = dans la ligne de commande.
Question 3)
Traduire ces distances angulaires en distances en UA, sachant que le système étoile et globules est à 2.0 kpc de la Terre.
Puis calculer les phases des globules, sachant que la période de la céphéide est P=41,44 jours.
[1 points]
Pour convertir sans douleur les distances angulaires en UA, voir
la définition du parsec
: Une distance de 1 UA vue à 1 pc sous-tend 1", donc N UA à p parsec
sous-tendent ...
La phase d'un globule est la distance du globule à l'étoile, mesurée en périodes de la céphéide. C'est donc le temps mis par la lumière pour aller de l'étoile au globule, divisé par la période de la céphéide.
N UA à p parsec sous-tendent N/p secondes d'arc.
Se repérer
Les cartes du ciel ci-jointes repèrent
les étoiles les plus brillantes par 2 coordonnées angulaires, pour 2 régions du ciel, sur l'équateur céleste ou proche du pôle nord céleste.
L'une de ces coordonnées angulaires, appelée ascension droite,
est exprimée en unités horaires (h, min, s).
La pleine échelle vaut 24 h, équivalant à 1
tour de ciel, ou 360 degrés.
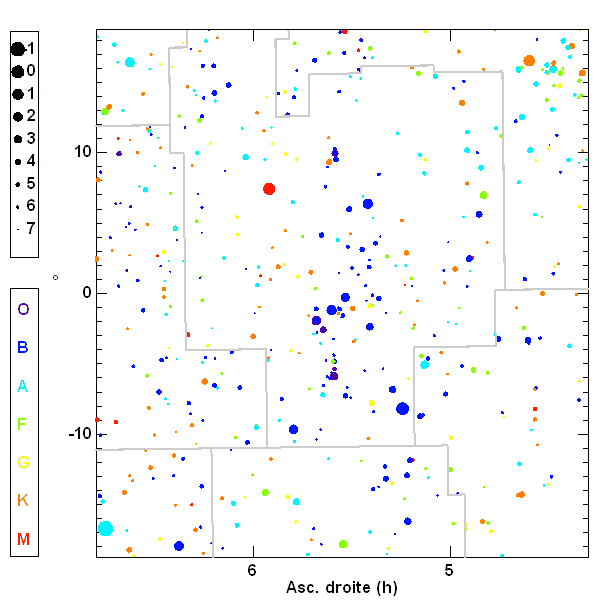
Carte du ciel, dans la région d'Orion. Les étoiles sont repérées par leurs coordonnées équatoriales (ascension droite en abscisse, déclinaison en ordonnée), analogues aux coordonnées géographiques (longitude, latitude) utilisées pour un lieu sur Terre.
Magnitudes
et
types spectraux sont également indiqués.
Crédit :
BSC/ASM
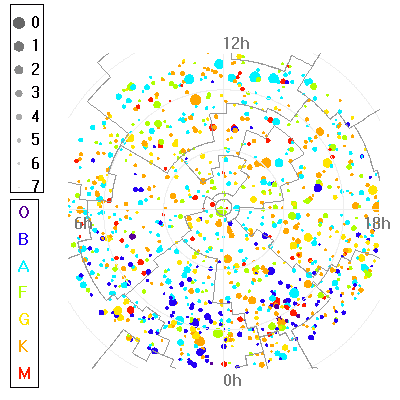
Carte du ciel, autour de l'étoile polaire. Les étoiles sont repérées par leurs coordonnées équatoriales, analogues aux coordonnées géographiques (longitude, latitude) utilisées pour un lieu sur Terre.
Crédit :
BSC/ASM

Carte des constellations de l'hémisphère Nord. On y reconnaît la Grande Ourse,
le Lion, le Triangle, les Gémeaux...
Crédit :
Bibliothèque de l'Observatoire de Paris
Constellations
Les constellations réunissent de façon arbitraire des étoiles voisines. Les histoires que racontent les constellations ou les groupes de constellation offrent un support à la mémoire.
Les tracés de constellation peuvent joindre les étoiles (la Grande Ourse devenant ainsi une casserole), ou peuvent les délimiter (les représentations du cours ont choisi cette convention de l'Union Astronomique Internationale).
Coordonnées équatoriales
Le ciel, sans la dimension de profondeur, est analogue à la surface d'une sphère. Usuellement,
on y repère un astre par son ascension droite et sa déclinaison. Ces 2 coordonnées sont définies dans un repère lié à la Terre : un des axes s'appuie sur l'axe polaire terrestre, l'autre sur l'équateur.
La déclinaison, équivalant à la latitude, varie de -90 à +90 degrés,
ces limites pointant respectivement les pôle sud et nord célestes.
L'ascension droite est comptée en heure, minute et seconde.
L'origine des ascensions droites est la direction du point vernal.
La conversion entre heure, minute et seconde d'une part, et degré,
minute d'arc et seconde d'arc d'autre part, est donnée par la
table ci-jointe.
La conversion entre heure, minute et seconde d'une part, et degré, minute d'arc et seconde d'arc d'autre part, est donnée par la table ci-jointe qui propose une conversion entre les unités horaires et angulaires. Le facteur 15 provient simplement de la division du jour (1 tour, ou 360 deg), en 24 heures, soit une rotation de 15 deg/h. Attention à bien respecter les unités, afin de ne pas confondre minute horaire et minute angulaire, qui ne sont pas égales.
Conversions angulaires
| 1 heure = 15 deg | 1 deg = 4 min | 1 deg = 0.0174 rad |
| 1 minute= 15' | 1 ' = 4 s | 1' = 0.29 mrad |
| 1 seconde= 15" | 1" = 1/15 s | 1" = 5 microrad |
Ecriture
Il est nécessaire de distinguer l'écriture décimale de l'écriture développée dans ces systèmes d'unités qui reposent sur une base non décimale.
Par exemple : 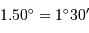 , mais
, mais 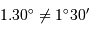
Conversion en radian
L'unité angulaire dans le système international d'unités (SI) est le radian. Vu l'usage intensif de la seconde d'arc en astronomie, il est utile d'avoir en tête l'ordre de grandeur :
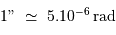
Cartographie
Exemple d'utilisation de l'appliquette : galaxie NGC1316, elliptique, en train de cannibaliser une petite galaxie elliptique.

Coordonnées
A l'aide du curseur, estimer les coordonnées angulaires des points du champ dans la constellation d'Orion, pour en déduire l'ordre de grandeur de ses dimensions angulaires.

Vérifier l'accord avec les coordonnées 2000 de 4 objets du champ, et repérer la nébuleuse d'Orion M42.
| étoile | 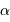 (h, min, s) (h, min, s) | 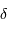 (deg, ', ") (deg, ', ") |
| Bételgeuse | 05 55 10 | +07 24 25 |
| Rigel | 05 14 32 | -08 12 06 |
| Bellatrix | 05 25 08 | +06 20 59 |
| M 42 | 05 35 17 | -05 23 28 |
Carte du ciel
Reprendre le relevé pour la carte synthétique de la région d'Orion.
Pourquoi l'accord est-il meilleur ?

 Un tour de ciel
Un tour de ciel
Difficulté : ☆
Temps : 20 min
En unité naturelle angulaire, le ciel, comme toute sphère, couvre 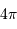 stéradians (pour s'en convaincre si besoin est, se rappeler l'aire de la sphère de rayon
stéradians (pour s'en convaincre si besoin est, se rappeler l'aire de la sphère de rayon 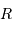 ). L'astronome préfère exprimer les angles en degré, heure et minute d'angle
). L'astronome préfère exprimer les angles en degré, heure et minute d'angle 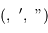 . Les instruments astronomiques ont des champs de vue qui varient typiquement de
. Les instruments astronomiques ont des champs de vue qui varient typiquement de 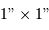 à
à 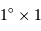 pour les instruments grand champ.
pour les instruments grand champ.
Question 1)
Traduire 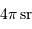 en degré carré, puis en minute et seconde carrée.
en degré carré, puis en minute et seconde carrée.
1 stéradian représente un angle solide de 1 radian par 1 radian : 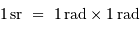
Ne pas oublier que :
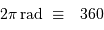 °
°
Question 2)
Un instrument imageur couvre un champ carré de 12' de côté (projet DENIS, mené à l'Observatoire Austral Européen (ESO), pour la cartographie infrarouge du ciel austral). Il pose en 3
couleurs dans l'infrarouge (filtres I, J, K à respectivement 0.85, 1.25 et 2.15 micromètres), avec des temps de pose de l'ordre de 10 à 30 s, soit environ 1 minute pour les 3 filtres. Il permet ainsi de cartographier une moitié du
ciel, jusqu'aux magnitudes limites 18.5 à 14.
Estimer la durée du programme d'observation (5 h/nuit pour compter
les aléas divers et météorologiques).
Se servir de la question précédente
 Détails lunaires
Détails lunaires
Difficulté : ☆☆
Temps : 20 min
La surface de la Lune a été observée par le système d'optique adaptative (OA) de l'ESO. Les clichés ci-joints permettent de comparer l'apport de cette technique. La largeur totale du champ représente 26", pour 201 pixels.
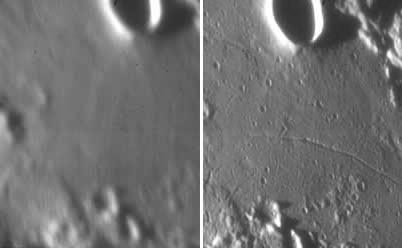
Avec optique adaptative (à droite), la surface de la Lune présente des détails inaccessibles sur l'image non corrigée
(système d'OA NAOS, développé pour le VLT à l'ESO). La largeur totale du champ représente 26".
Crédit :
ESO

Question 1)
Quelle est la taille angulaire d'un pixel ? En déduire la taille
linéaire, en km, du champ de vue d'un pixel et du champ de vue
total, la Lune étant à 384 000 km de la Terre lors de
l'observation.
[2 points]
L'unité naturelle des angles est le radian.
Question 2)
À l'aide de l'appliquette, estimer le diamètre apparent du gros cratère, les tailles des plus petits détails visibles, avec ou sans optique adaptative.
[1 points]
La conversion d'unité peut être introduite dans la fenêtre rapport d'unité.

Rotation du ciel, ou de la Terre ? La régularité du mouvement en fait une "bonne" horloge.
Crédit :
CFHT
La rotation de la Terre
La mesure du temps, comme la définition des unités de temps, s'appuie sur des rotations régulières : la rotation propre de la Terre, sa révolution autour du Soleil.
Nombre de diviseurs de la base
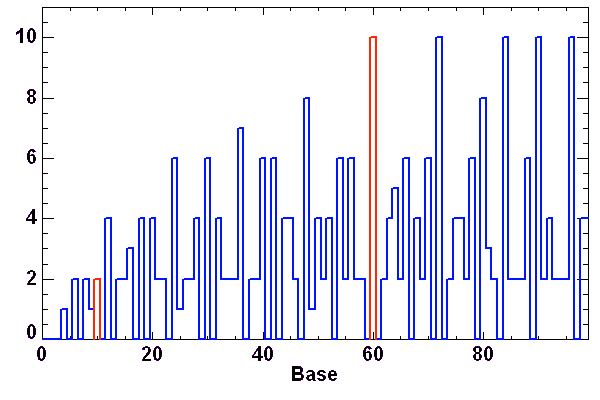
Le décompte du nombre de diviseurs de la base utilisée (1 et la base non compris) montre que 60 présente un maximum local prononcé, et que c'est le premier nombre à atteindre 10 diviseurs.
Crédit :
ASM
Heure, minute et seconde
La découpe des jours en 24 heures est une longue histoire... A l'époque où le temps n'était défini qu'à la précision d'une clepsydre ou d'un cadran solaire, la définition même de l'heure est restée vague, et sa durée variable.
Quantitativement, la base 24 provient des Egyptiens, pour qui 24 h = 12 h de jour + 12 h de
nuit, avec 12 = 1 + 10 + 1. Le jour et la nuit égyptiens comptaient
invariablement 10 heures, auxquelles étaient rajoutées 2 heures extrêmales
"entre chien et loup".
Pourquoi compte-t-on 60 secondes par minute, et 60 minutes par heure ?
Plus encore que pour l'heure, l'usage des minutes et secondes est récent (XVIIe siècle), vu qu'il nécessite un chronométrage précis du temps.
Quantitativement, la base 60 provient d'un héritage babylonien, et date de la fin du 3e millénaire avant notre ère. Le nombre 60 présente en effet l'avantage de posséder un grand nombre de diviseurs (2, 3, 4, 5, 6, 10, 12, 15, 20, 30), ce qui est commode pour les calculs de fraction lorsque les techniques de calcul d'une division ne sont pas connues.
C'est pour cette raison que 60 servait de base de calcul, en complément ou à la place de la base 10 ; cet usage a perduré de nos jours pour les mesures de temps et d'angles.
La mesure du temps
La mesure du temps s'est longtemps appuyée sur les mouvements les plus réguliers observables : la rotation propre de la Terre (le jour), sa révolution autour du Soleil (l'année). Ce n'est qu'en 1969 que le Bureau international des poids et mesures a abandonné la rotation de la Terre pour la définition de la seconde comme unité de temps.
La seconde correspond à l'intervalle de temps comprenant
9 192 631 770 oscillations entre les deux niveaux hyperfins de l'état fondamental de l'atome de césium 133.
Durées
Il n'y a pas d'unités temporelles spécifiques en astrophysique, contrairement aux nombreuses unités de distance.
La seconde apparaît une unité ni mieux ni moins bien appropriée que pour d'autres domaines que la physique.
L'année est de facto une unité pratique pour les problématiques circum-stellaires, vu qu'elle a été définie comme unité "circumsolaire".
Il suffit juste de s'habituer, dans certains cas, à l'usage des grands nombres, et de compter en millions, voire milliards d'années.
Temps de lumière
L'usage du temps de lumière est sans ambiguïté, dès lors que la célérité de la lumière est une constante universelle. Un temps de lumière est une distance, et correspond à la durée du trajet si l'on chevauche un photon.
 Définition
Définition
La célérité de la lumière dans le vide est un invariant, fixé par définition à 299 792 458 m/s.
 Echelle de temps dynamique
Echelle de temps dynamique
Difficulté : ☆☆
Temps : 20 min
On considère un objet autogravitant de masse 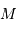 , rayon
, rayon 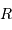 , et on s'intéresse à son échelle de temps dynamique.
, et on s'intéresse à son échelle de temps dynamique.
Question 1)
Quelle constante fondamentale de la physique intervient nécessairement dans toute formulation de la physique du problème.
Il s'agit ici de gravitation.
Question 2)
Montrer, avec le minimum de calcul possible, que 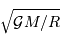 est homogène à une vitesse, et en déduire que
est homogène à une vitesse, et en déduire que 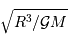 est homogène à un temps.
est homogène à un temps.
Essayez de dénicher une loi physique qui exprime une vitesse dans un problème gouverné par la gravitation.
L'accélération normale d'un satellite en orbite circulaire peut s'écrire en fonction du champ gravitationnel, à la distance 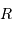 :
:
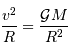
Question 3)
Montrer que 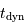 peut s'exprimer en fonction de la masse volumique moyenne
peut s'exprimer en fonction de la masse volumique moyenne 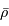 de l'objet.
de l'objet.
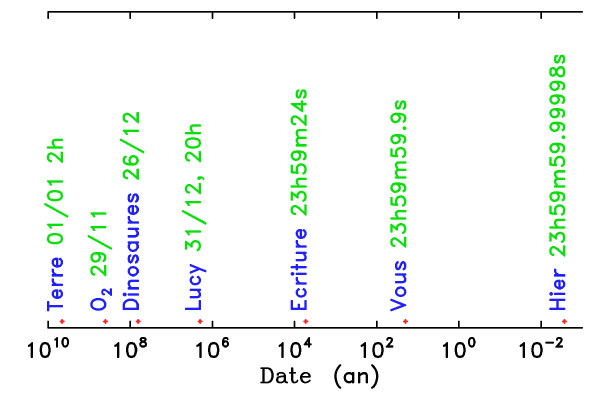
 La vie du Soleil en 1 an seulement
La vie du Soleil en 1 an seulement
Difficulté : ☆
Temps : 30 min
Quelques événements
| La formation du système solaire | en 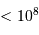 an après le Soleil an après le Soleil |
| L'apparition du dioxygène atmosphérique | 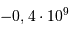 an an |
| La disparition des dinosaures | 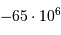 an an |
| Notre ancêtre Lucy | 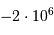 an an |
| La maîtrise de l'écriture | 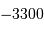 avant JC avant JC |
| Votre naissance | ... |
| Hier | |
Question 1)
Reporter dans un graphe en échelle logarithmique les
événements suivants de l'histoire de la Terre depuis la naissance du Soleil [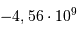 an].
an].
Déterminer leur date, sur la base d'une année, la formation du Soleil débutant le 1er janvier à 0 heure, et aujourd'hui correspondant à minuit du 31 décembre.
Aller chercher une calculatrice !
 Durée d'effondrement
Durée d'effondrement
Difficulté : ☆☆
Temps : 20 min
L'échelle de temps dynamique d'un objet autogravitant donne un bon ordre de grandeur de la durée caractéristique de l'éventuel effondrement de cet objet.
| Masse (kg) | Rayon (km) |
| Soleil | 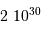 | 700 000 |
| Étoile à neutrons | 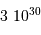 | 10 |
| Nuage d'hydrogène moléculaire | 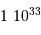 | 10 AL |
Question 1)
Rappeler l'expression de cette échelle de temps, fonction de la
masse 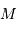 , du rayon
, du rayon 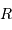 et de la constante gravitationnelle
et de la constante gravitationnelle 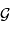 .
.
[2 points]
Question 2)
Calculer l'échelle de temps pour les 3 objets proposés. Commenter.
[3 points]
 Quelle source d'énergie ?
Quelle source d'énergie ?
Difficulté : ☆☆
Temps : 20 min
Question 2)
En déduire l'échelle de temps associée à ce réservoir d'énergie. Est-elle compatible avec l'âge du Soleil ?
[2 points]
Question 3)
On s'intéresse au réservoir d'énergie nucléaire. Le rendement énergétique de la fusion de l'hydrogène en hélium est de 0.007, ce qui signifie que la fusion d'une masse 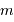 d'hydrogène dégage une énergie
d'hydrogène dégage une énergie 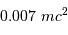 . On estime, pour une étoile telle que le Soleil, qu'un dixième seulement de sa masse fusionnera.
En déduire une estimation de la durée de vie du Soleil.
. On estime, pour une étoile telle que le Soleil, qu'un dixième seulement de sa masse fusionnera.
En déduire une estimation de la durée de vie du Soleil.
[2 points]
Cette section a permis d'introduire des ingrédients indispensables pour un champ d'activité fécond de l'astrophysique : l'étude des objets binaires dans le voisinage solaire (cf systèmes binaires et multiples).
Pour un tel système binaire, repéré par 2 angles directement obtenus par l'observation (parallaxe 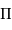 et séparation angulaire
et séparation angulaire 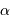 ) et mesurés en seconde d'angle, on connaît alors immédiatement la distance en parsec :
) et mesurés en seconde d'angle, on connaît alors immédiatement la distance en parsec :
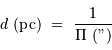
et la séparation linéaire en unité astronomique :
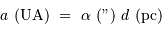
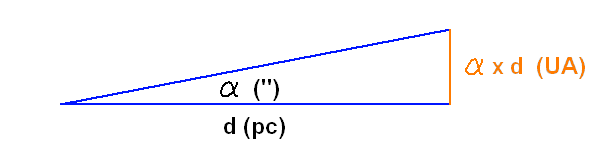
Relation dans un triangle, avec une distance en parsec, un angle en seconde d'arc, et une mesure en UA.
Crédit :
ASM
- Question 1
Aide :
Calculatrice !
Solution :
Le rapport d'échelle pour passer du Soleil à la pomme, est de l'ordre de
10 milliards à 1, la moitié si l'on tient compte du fait qu'est donné le rayon du Soleil, mais le diamètre de la pomme (ce n'est pas le facteur 2 de différence qui importe ici, mais les ordres de grandeur).
Le rayon terrestre étant 100 fois plus petit que celui du Soleil,
il s'ensuit un rayon équivalent pour la Terre de l'ordre de 0.7 mm.
Un bout de pépin !
- Question 2
Aide :
Voir la page de cours !
Solution :
La conversion des pc en m donne une distance de l'ordre de 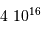 m ; en tenant compte du rapport
m ; en tenant compte du rapport 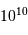 , cela donne une distance de
4000 km.
, cela donne une distance de
4000 km.
La première pomme étant en France,
la pomme la plus proche est, au choix, presque aux Etats-Unis, en Afrique équatoriale, ou en Inde. Entre les 2 pommes, il y a de tout petits noyaux
(Jupiter, Saturne...), et des bouts de pépins (la Terre...), quelques
poussières et microbes (les astéroïdes et comètes), et aussi et surtout du vide.
- Question 1
Aide :
Déterminer le volume balayé par le vaisseau, nécessaire pour traverser la galaxie de part en part sans "toucher" une seule étoile.
Aide :
Ce volume est cylindrique ; son rayon dépend surtout de la taille des étoiles, pas de celle du véhicule, car il est très petit par rapport à une étoile.
Aide :
Comparer le volume précédemment trouvé au volume moyen offert à une étoile.
Solution :
Pour éviter toute mauvaise surprise, le vaisseau ne doit pas voir d'étoile, repérée par son centre, dans une section de rayon 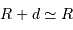 (car
(car 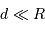 ).
).
Le volume 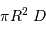 doit donc être libre de toute étoile. La
probabilité d'en trouver une s'énonce
doit donc être libre de toute étoile. La
probabilité d'en trouver une s'énonce 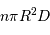 , avec
, avec 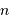 la densité
stellaire. L'application numérique donne donc, avec
la densité
stellaire. L'application numérique donne donc, avec 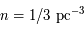 , et
, et 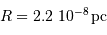 ,
, 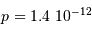 .
.
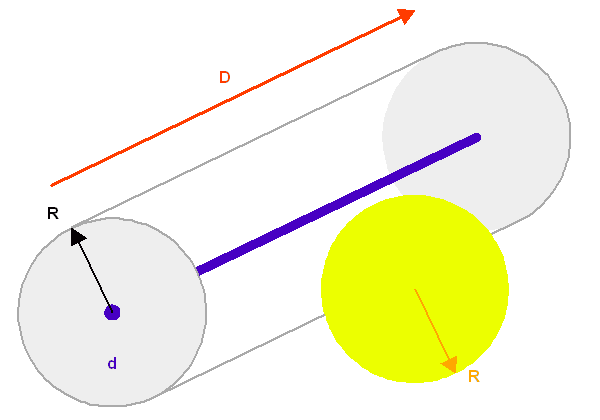
Crédit :
ASM
- Question 2
Aide :
Bien répertorier les conditions du voyage : risque de collisions, durée du trajet, pause sandwich...
Aide :
Que voit-on exactement d'une étoile : un point, un disque, une tache de diffraction ? Et combien d'étoiles a-t-on sur un pixel ?
Solution :
Le risque de collision est minime, mais le temps de parcours ne saurait être inférieur, pour vos amis n'étant pas du voyage, à 17 000 ans (5.4 kpc 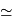 17 000 AL). Pour vous, pilote, cette durée dépend de votre vitesse : mieux vaut être relativiste, pour ne pas trop vieillir !
17 000 AL). Pour vous, pilote, cette durée dépend de votre vitesse : mieux vaut être relativiste, pour ne pas trop vieillir !
D'un point de vue observationnel, les étoiles ne sont pas des points matériels, mais des taches de diffraction. La densité stellaire est alors telle qu'il est impossible de résoudre spatialement ces objets : ces taches de diffraction des étoiles se superposent et contribuent à l'aspect uniformément brillant du bulbe.
- Question 1
Aide :
Il s'agit ici de gravitation.
Solution :
Dès lors que l'on parle de la gravitation, intervient la constante gravitationnelle 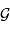 .
.
- Question 2
Aide :
Essayez de dénicher une loi physique qui exprime une vitesse dans un problème gouverné par la gravitation.
Aide :
L'accélération normale d'un satellite en orbite circulaire peut s'écrire en fonction du champ gravitationnel, à la distance 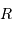 :
:
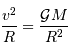
Solution :
Il est plus simple de procéder par induction, plutôt que de chercher des exposants 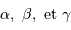 qui satisfassent à :
qui satisfassent à :
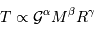
On écrit p.ex. que l'accélération normale d'un satellite en orbite circulaire à la distance 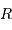 est égale au champ gravitationnel :
est égale au champ gravitationnel :
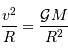
D'où il sort une vitesse caractéristique (que l'on rencontre dans tout problème gravitationnel, à une constante numérique près que l'analyse dimensionnelle ne permet pas de calculer)
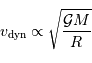
Le temps dynamique ne peut être que de la forme
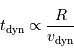
et donc
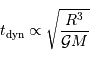
- Question 3
Aide :
Définir 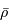 en fonction de
en fonction de 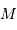 et
et 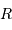
Solution :
La masse volumique moyenne est proportionnelle à la masse 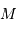 divisée par le volume
divisée par le volume 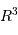 :
:
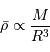
et donc le temps dynamique s'exprime :
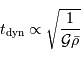
- Question 4
Aide :
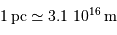
Solution :
Les application numériques donnent :
- noyau cométaire : 31 400 s, soit presque 9 h
- la Terre : 5100 s, soit 1h 25min
- la Voie Lactée : 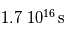 , soit environ 500 millions d'années
, soit environ 500 millions d'années
La constante de temps dynamique d'un noyau cométaire est plus longue que celle de la Terre, car la masse volumique moyenne 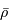 est plus faible.
est plus faible.
La constante de temps dynamique d'une galaxie représente une fraction non négligeable de l'âge de l'Univers. Elle donne l'ordre de grandeur de sa période de rotation moyenne.
La constance de temps dynamique pour la Terre représente l'ordre de grandeur d'une foultitude de phénomènes :
- la période typique d'un satellite en orbite basse (1h40 en fait)
- la durée typique d'un vol de missile balistique
- la durée typique de propagation d'une secousse sismique de l'épicentre du séisme aux antipodes
- un match de foot... mais ça c'est un hasard

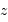 ; ce qui nécessite une
; ce qui nécessite une 







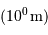 : le
: le 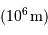 : taille caractéristique de la
: taille caractéristique de la
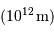 : diamètre d'une
: diamètre d'une 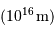 : taille d'une
: taille d'une 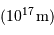 : diamètre d'un
: diamètre d'un 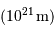 : diamètre d'une
: diamètre d'une 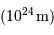 : à l'échelle d'un
: à l'échelle d'un 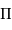 mesure le demi-grand axe angulaire de ce mouvement apparent.
mesure le demi-grand axe angulaire de ce mouvement apparent.

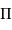 , exprimée en seconde d'arc, est à une distance
, exprimée en seconde d'arc, est à une distance 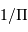 , exprimée en parsec.
, exprimée en parsec.
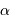 exprimée en seconde d'arc vu à une distance
exprimée en seconde d'arc vu à une distance 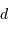 exprimée en parsec possède une taille linéaire
exprimée en parsec possède une taille linéaire 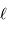 , exprimée en unité astronomique (dans l'approximation des petits angles) :
, exprimée en unité astronomique (dans l'approximation des petits angles) :
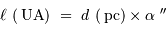
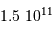
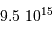
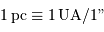
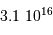



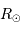
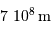
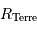
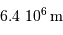
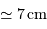
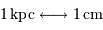
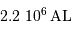 et de taille comparable à notre galaxie, et le Grand Nuage de Magellan,
situé à
et de taille comparable à notre galaxie, et le Grand Nuage de Magellan,
situé à 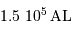 et de diamètre
et de diamètre 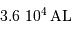 . Respecter une même échelle pour les tailles et distances.
. Respecter une même échelle pour les tailles et distances.
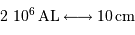
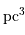 . On suppose que ces étoiles sont toutes de même type, de rayons
. On suppose que ces étoiles sont toutes de même type, de rayons 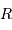 identiques.
identiques.
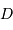
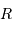
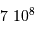 m
m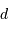
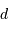 traversant le bulbe de part en part.
traversant le bulbe de part en part.


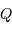 le quasar et
le quasar et 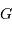 l'amas de galaxies et T la Terre.
l'amas de galaxies et T la Terre.


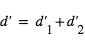 correspondant au trajet dévié quasar-lentille-Terre. On note
correspondant au trajet dévié quasar-lentille-Terre. On note 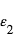 le petit angle entre l'image directe et l'image déviée.
le petit angle entre l'image directe et l'image déviée.
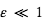 ,
, 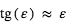 et
et 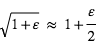
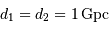 et
et 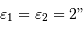 . Donner le résultat en pc ainsi qu'en temps de lumière.
. Donner le résultat en pc ainsi qu'en temps de lumière.
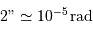

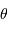 de chaque globule et remplir la colonne correspondante du tableau présenté par la 2ème appliquette.
de chaque globule et remplir la colonne correspondante du tableau présenté par la 2ème appliquette.



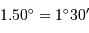 , mais
, mais 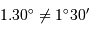
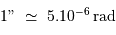
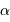 (h, min, s)
(h, min, s) 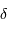 (deg, ', ")
(deg, ', ") 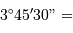
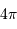 stéradians (pour s'en convaincre si besoin est, se rappeler l'aire de la sphère de rayon
stéradians (pour s'en convaincre si besoin est, se rappeler l'aire de la sphère de rayon 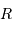 ). L'astronome préfère exprimer les angles en degré, heure et minute d'angle
). L'astronome préfère exprimer les angles en degré, heure et minute d'angle 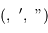 . Les instruments astronomiques ont des champs de vue qui varient typiquement de
. Les instruments astronomiques ont des champs de vue qui varient typiquement de 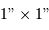 à
à 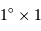 pour les instruments grand champ.
pour les instruments grand champ.
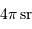 en degré carré, puis en minute et seconde carrée.
en degré carré, puis en minute et seconde carrée.
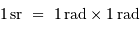
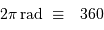 °
°

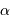 petite correspond, à une distance
petite correspond, à une distance 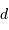 , à la taille linéaire
, à la taille linéaire 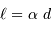 . Mais il faut travailler dans le bon système d'unités.
. Mais il faut travailler dans le bon système d'unités.


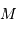 et rayon
et rayon 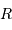 , un phénomène gouverné par la gravitation aura naturellement une constante de temps de l'ordre de
, un phénomène gouverné par la gravitation aura naturellement une constante de temps de l'ordre de 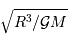 (vérification proposée en
(vérification proposée en 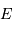 et
émettant une luminosité totale (càd une puissance)
et
émettant une luminosité totale (càd une puissance) 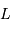 peut le faire pendant typiquement la durée
peut le faire pendant typiquement la durée 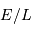 .
.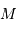 , rayon
, rayon 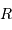 , et on s'intéresse à son échelle de temps dynamique.
, et on s'intéresse à son échelle de temps dynamique.
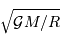 est homogène à une vitesse, et en déduire que
est homogène à une vitesse, et en déduire que 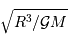 est homogène à un temps.
est homogène à un temps.
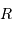 :
:
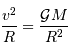
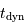 peut s'exprimer en fonction de la masse volumique moyenne
peut s'exprimer en fonction de la masse volumique moyenne 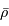 de l'objet.
de l'objet.
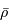 en fonction de
en fonction de 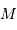 et
et 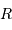
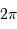 :
:
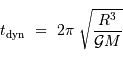
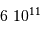
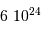
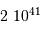
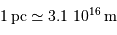
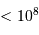 an après le Soleil
an après le Soleil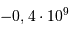 an
an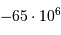 an
an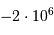 an
an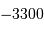 avant JC
avant JC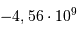 an].
an].
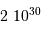
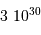
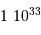
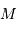 , du rayon
, du rayon 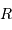 et de la constante gravitationnelle
et de la constante gravitationnelle 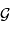 .
.
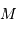 , du rayon
, du rayon 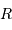 du Soleil, et de la constante gravitationnelle
du Soleil, et de la constante gravitationnelle 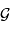 . Faire l'application numérique.
. Faire l'application numérique.
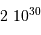
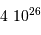
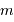 d'hydrogène dégage une énergie
d'hydrogène dégage une énergie 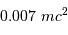 . On estime, pour une étoile telle que le Soleil, qu'un dixième seulement de sa masse fusionnera.
En déduire une estimation de la durée de vie du Soleil.
. On estime, pour une étoile telle que le Soleil, qu'un dixième seulement de sa masse fusionnera.
En déduire une estimation de la durée de vie du Soleil.
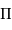 et séparation angulaire
et séparation angulaire 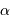 ) et mesurés en seconde d'angle, on connaît alors immédiatement la distance en parsec :
) et mesurés en seconde d'angle, on connaît alors immédiatement la distance en parsec :
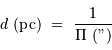
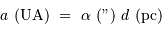
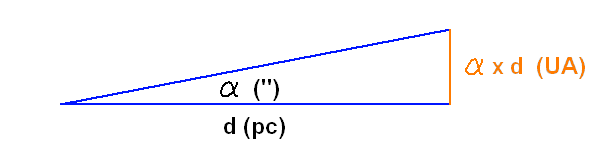
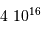 m ; en tenant compte du rapport
m ; en tenant compte du rapport 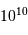 , cela donne une distance de
4000 km.
, cela donne une distance de
4000 km.
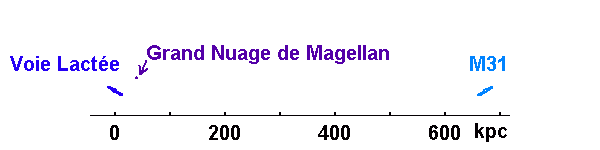
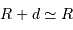 (car
(car 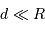 ).
).
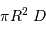 doit donc être libre de toute étoile. La
probabilité d'en trouver une s'énonce
doit donc être libre de toute étoile. La
probabilité d'en trouver une s'énonce 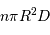 , avec
, avec 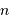 la densité
stellaire. L'application numérique donne donc, avec
la densité
stellaire. L'application numérique donne donc, avec 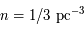 , et
, et 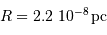 ,
, 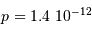 .
.

 17 000 AL). Pour vous, pilote, cette durée dépend de votre vitesse : mieux vaut être relativiste, pour ne pas trop vieillir !
17 000 AL). Pour vous, pilote, cette durée dépend de votre vitesse : mieux vaut être relativiste, pour ne pas trop vieillir !
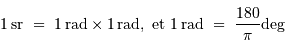
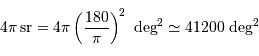
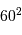 , on trouve
, on trouve 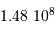 minutes d'angle
carrées, et
minutes d'angle
carrées, et 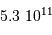 secondes d'angle carrées.
secondes d'angle carrées.
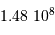 minutes d'angle
carrées, un hémisphère représente
minutes d'angle
carrées, un hémisphère représente 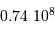 champs de 1' par 1', soit
champs de 1' par 1', soit
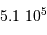 champs de 12' par 12'.
champs de 12' par 12'.
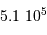 minutes, ou de l'ordre de 8400 h.
minutes, ou de l'ordre de 8400 h.
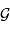 .
.
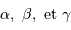 qui satisfassent à :
qui satisfassent à :
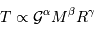
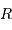 est égale au champ gravitationnel :
est égale au champ gravitationnel :
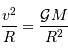
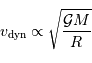
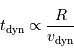
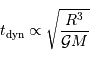
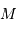 divisée par le volume
divisée par le volume 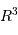 :
:
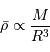
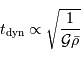
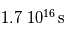 , soit environ 500 millions d'années
, soit environ 500 millions d'années
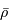 est plus faible.
est plus faible.