Le décalage spectral pour mesurer les distances des galaxies

Auteur: François Hammer

A l'exception de la grande galaxie d'Andromède et de quelques galaxies naines proches, toutes les galaxies s'éloignent de nous. Pour mesurer les distances des galaxies, les astronomes utilisent la relation établie par l'astronome américain Edwin Hubble, qui montre que la vitesse v d'éloignement des galaxies est proportionnelle à leurs distances, D, selon v=H₀D, ou H₀ est la constante de Hubble. Plus une galaxie est lointaine, plus vite elle s'éloigne de nous. Son émission lumineuse est alors affectée par sa vitesse d'éloignement, à cause de l'effet Doppler. Ce même effet s'applique aux ondes acoustiques : lorsqu'une ambulance se rapproche de nous, la longueur d'onde acoustique est diminuée (le son devient plus aigu), et lorsqu'elle s'éloigne, elle s'agrandit (le son devient plus grave). De même, la lumière émise par une galaxie s'éloignant de nous sera décalée vers le rouge (augmentation de la longueur d'onde) avec un décalage spectral z donné par :

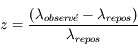
$z=\frac{(\lambda_{observ\'e} - \lambda_{repos})}{\lambda_{repos}}$

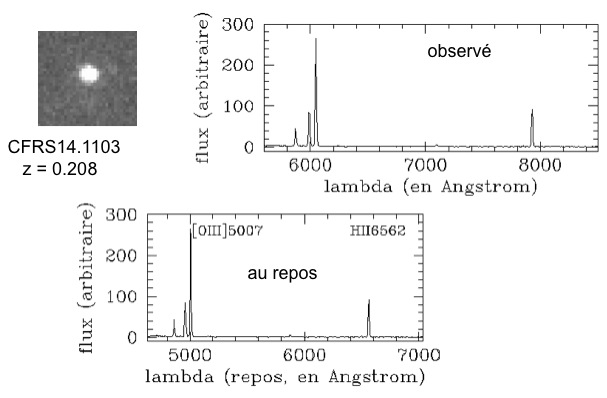
Pour mesurer le décalage spectral, les astronomes utilisent les spectres des galaxies (voir Figure). Ils en déduisent la vitesse des galaxies, avec :

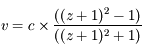$v=c\times \frac{((z+1)^{2}-1)}{((z+1)^{2}+1)}$ , où c est la vitesse de la lumière, c=300 000 km/s.

Lorsque la vitesse d'éloignement est petite par rapport à la vitesse de la lumière, on peut simplifier l'expression ci-dessus par v=cz. Connaissant la vitesse d'éloignement d'une galaxie, on en déduit sa distance, D=v/H₀.

Spectre d'une galaxie s'éloignant à une vitesse de 56000 km/s

Observation du spectre d'une galaxie, CFRS14.1103, située à environ 3 milliards d'années-lumière. Le spectrographe décompose l'émission de la lumière en fonction de la longueur d'onde (lambda), de la même manière qu'un prisme décompose la lumière en différentes couleurs. Le gaz ionisé de cette galaxie émet un rayonnement sous forme de raies spectrales à des longueurs d'ondes observées de 5007 et de 6562 Angstroms (1 Angstrom=1 dix milliardième de mètre) pour l'Oxygène et l'Hydrogène ionisés (raies [OIII] et Hα, voir spectre en bas de la figure). Ces émissions sont observées à 6048 et 7927 Angstroms dans le spectre de la galaxie CFRS14.1103 (spectre en haut de la figure). On en déduit le décalage spectral de cette galaxie, z=0,208, sa vitesse d'éloignement v=56000 km/s et sa distance, D=2,74 milliards d'années-lumière.

Crédit : ASM/François Hammer