Apprendre

Objectifs

Estimer quelques dimensionnements des objets sur la séquence principale à partir de la relation masse-luminosité sur séquence principale (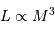 $L \propto M^3$ ).

Relation masse luminosité

En faisant de la physique avec les mains, on démontre rapidement que la luminosité d'une étoile est reliée à sa masse par la relation :

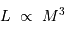
$L \ \propto\ M^3$

La démonstration complète est hors de portée de ce cours, car elle introduit des éléments de transfert radiatif, qui aboutissent à la relation entre masse et rayon stellaires. Notons les étapes principales.

Constante de temps radiative

La luminosité d'une étoile, commensurable à une puissance, est égale au quotient de l'énergie interne du gaz de photons à la constante de temps radiative :

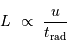
$L\ \propto\ {u\over t _{\mathrm{rad}}}$

L'énergie interne du gaz de photons est proportionnelle au volume stellaire 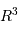R^3 , ainsi qu'à 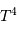T^4 selon la loi de rayonnement du corps noir). La constante de temps radiative mesure le durée d'échappement des photons, qui résulte d'un phénomène stochastique.

On suppose que le libre parcours moyen 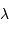$\lambda$ d'un photon est uniforme dans tout l'intérieur stellaire. Le processus de marche au hasard demande alors, pour parcourir une distance 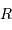par étapes de longueur élémentaire 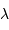$\lambda$ , un nombre d'étapes variant comme 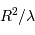$R^2 / \lambda$ . On en déduit la constante de temps radiative :

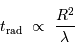
$t _{\mathrm{rad}} \ \propto\ {R^2\over \lambda}$

Comme le libre parcours 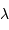$\lambda$ est en fait inversement proportionnel à l'encombrement, donc à la masse volumique, on a :

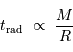
$t _{\mathrm{rad}} \ \propto\ {M\over R}$

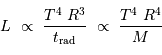
$L\ \propto\ {T^4 \ R^3\over t _{\mathrm{rad}}} \ \propto\ {T^4 \ R^4\over M}$

Relation masse-rayon-température-luminosité

Dans les pages précédentes, des éléments de physique simples ont permis de calibrer les masse volumique et pression internes :

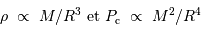
$\rho\ \propto\ M/R^3 \ \mathrm{ et } \ P _{\mathrm{c}}\ \propto\ M^2/R^4$

ainsi que la relation donnant la température centrale :

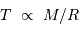
$T\ \propto\ M/R$

La luminosité du corps noir stellaire vérifie donc :

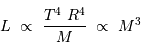
$L\ \propto\ {T^4 \ R^4\over M}\ \propto\ M^3$

Observationnellement, l'exposant s'avère être 3.3 :

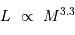
$L \ \propto\ M^{3.3}$

Durée de vie sur la séquence principale

Cette relation, avec un exposant élevé, signifie qu'une étoile massive va être très lumineuse. Son réservoir de matière étant limité, elle évoluera et mourra beaucoup plus vite qu'une étoile moins massive. Les étoiles les plus massives évoluent en une dizaine de millions d'années. En revanche, une étoile très peu massive a une espérance de vie très longue, se chiffrant en dizaines de milliards d'années.

Avec le réservoir d'énergie donnée par la masse, et la luminosité variant comme 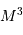M^3 , la durée de vie stellaire varie comme :

$t _{\mathrm{vie}} \simeq {E _{\mathrm{nucl}} \over L} \propto {M\over M^3} = {1\over M^2}$

Durée de vie
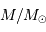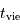étoile	$M/M_\odot$	$t _{\mathrm{vie}}$ (ans)
naine de type M	0.08	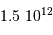$1.5 \ 10^{12}$	100 fois l'âge de l'Univers
Soleil	1	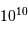$10^{10}$	le Soleil est à mi-vie
naine de type O	40	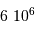$6\ 10^6$	très court !

Ordre de grandeur de la durée de vie d'une étoile en fonction de sa masse.