Ex: Précession du périastre

Auteur: S. Renner

Précession du périastre

Difficulté : ☆ Temps : 1h30

On considère le mouvement d'un satellite de masse 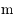$m$ par rapport à un corps central de masse 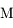$M$ et de rayon 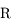$R$ . On note 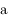$a$ le demi-grand axe du satellite, 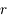sa distance au corps central, et 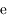$e$ son excentricité supposée faible (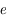<<1).

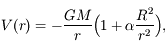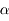Sous l'effet de sa rotation, le corps central est légèrement aplati aux pôles. En conséquence, le potentiel gravitationnel pour un satellite évoluant dans le plan équatorial est donné par : $\displaystyle V(r)= - \frac{G M}{r} \Big{(} 1 + \alpha \frac{R^2}{r^2} \Big{)},$ où $\alpha$ est une constante <<1 qui caractérise l'applatissement. 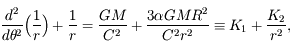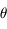On peut montrer qu'alors l'équation du mouvement du satellite s'écrit: $\displaystyle \frac{d^2}{d\theta^2} \Big{(} \frac{1}{r} \Big{)} + \frac{1}{r} = \frac{GM}{C^2} + \frac{3 \alpha GM R^2}{C^2 r^2} \equiv K_1 + \frac{K_2}{r^2},$ où $\theta$ est la position angulaire du satellite sur sa trajectoire (anomalie vraie), et 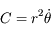$C=r^2 \dot{\theta}$ le moment cinétique.

Question 1)

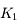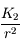Comparer K_1 et $\frac{K_2}{r^2}$ , et en déduire que la trajectoire du satellite est peu modifiée sous l'effet de l'applatissement du corps central, par rapport au problème à 2 corps classique.

Solution

Question 2)

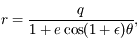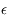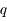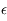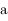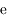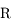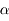Montrer que la solution de l'équation du mouvement peut s'écrire: $\displaystyle r = \frac{q}{1+e \cos (1+ \epsilon) \theta},$ avec $\epsilon$ <<1, et exprimer et $\epsilon$ en fonction de $a$ , $e$ , $R$ et $\alpha$ .

Solution

Question 3)

Quelle est alors l'allure de la trajectoire? Exprimer l'avance 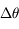$\Delta \theta$ du périastre de la trajectoire, c'est-à-dire l'angle dont les axes de l'ellipse ont tourné après une révolution du satellite.

Solution

Question 4)

Déterminer:

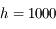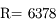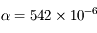a) l'avance du périgée d'un satellite artificiel d'altitude h=1000 km autour de la Terre ( $R= 6378$ km, $\alpha=542 \times 10^{-6}$ ).

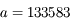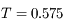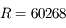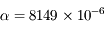b) l'avance du périastre du satellite Pan ( a=133583 km et période orbitale T=0.575 jours) autour de Saturne ( R=60268 km, $\alpha=8149 \times 10^{-6}$ ).

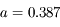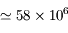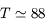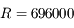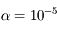c) l'avance du périhélie de Mercure ( a=0.387 UA $\simeq 58 \times 10^{6}$ km, $T \simeq 88$ jours) autour du Soleil ( R=696000 km, $\alpha = 10^{-5}$ ). La précession observée du périhélie de Mercure s'élève en fait à 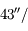43''/ siècle. Commenter.

Solution