Ex: Trajectoire balistique dans le système solaire |
Trajectoire balistique dans le système solaireDifficulté : ☆☆ Temps : 1h30
Une conique est défine par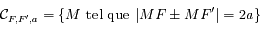 
. Préciser le cas d'une ellipse et le cas d'une hyperbole. Pour ce dernier cas, préciser aussi comment sont distinguées les deux branches de l'hyperbole.
Montrer que le second foyer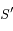 
se trouve sur une hyperbole 
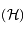de foyers 
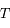et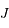 
passant par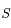 
Donner la nature de la conique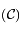 
suivant la branche de 
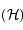sur laquelle se trouve 
.
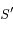On pose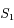 
le point de 
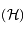symétrique de 
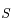par rapport à l'axe focal.
Montrer qu'aucune trajectoire physique n'est possible quand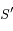 
se trouve entre 
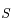et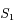 
.
On fixe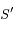 
sur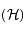 
, exprimer le demi-grand axe 
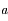et l'excentricité 
de la conique 
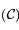en fonction des distances entre les points 
, 
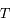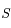et 
 |  |
quand
tend vers 
tend vers 
tend vers l'infini sur la même branche
