Ex : les solutions du problème de deux corps |
Les solutions du problème de deux corpsDifficulté : ☆ Temps : 1 h
Montrer que si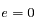 
la solution est un cercle dont on déterminera le rayon.
Montrer que dans tous les autres cas, il existe un minimum pour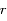 
que l'on déterminera et que l'on notera 
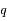. La position pour laquelle cette distance est atteinte s'appelle le péricentre.
A quoi correspond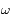 
?
Quand est-il pour le maximum de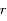 
? La position pour laquelle cette distance, notée 
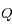, est atteinte s'appelle apocentre lorsqu'elle existe.
On se place maintenant dans un repère orthonormé direct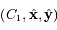 
où l'axe des abscisses 
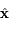est dirigé vers le pericentre. Pour un point 
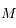du plan on note 
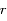la distance 
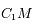et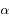 
l'angle entre l'axe des abscisses et le vecteur 
.
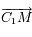Ecrire l'équation de la solution générale du problème de 2 corps en utilisant les coordonnées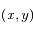 
de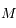 
dans le repère 
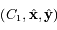.On remarquera que l'équation obtenue est léquation générale d'une conique.
Montrer que si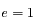 
on obtient l'équation d'une parabole dont on déterminera les coordonnées du péricentre.
Montrer que si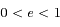 
on obtient l'équation d'une ellipse dont on déterminera le centre, le demi-grand axe et le demi-petit axe.
Montrer que si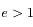 
on obtient l'équation d'une hyperbole dont on déterminera le péricentre et les asymptotes.
 |  |
ce qui est bien l'équation d'un cercle de centre 
et de rayon 
.
sera minimal quand 
sera maximal, c'est à dire lorsque ![\theta=\omega \,\,\,{\rm mod}\,[2\pi]](../pages_coniques/equations_coniques/equation62.png)
. Dans ce cas on a 
.
sera maximal quand 
sera minimal, c'est-à-dire lorsque ![\theta=\omega+\pi \,\,\,{\rm mod}\,[2\pi]](../pages_coniques/equations_coniques/equation66.png)
. Or si 
on s'aperçoit que dans ce cas 
n'est pas défini, et si 
alors 
est négatif ce qui n'a pas de sens.
Lorsqu'il est défini (
), on a 
. On remarque que l'apocentre se trouve à l'opposé du péricentre.
et 
l'équation devient :
.
Avec 
on a:
qui se transforme facilement en 
. On obtient finalement
qui est l'équation d'une conique.
,
.
.
qui devient :
et 
(qui est défini puisque 
), l'équation
devient:
, de demi-grand axe 
et de demi-petit axe 
.
et 
(qui est défini puisque cette fois 
). Ainsi l'équation devient:
, et d'asymptotes :
.