Ex: Masse du trou noir central de la galaxie |
Masse du trou noir central de la galaxieDifficulté : ☆☆ Temps : 1h30
Localiser le centre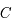 
de l'ellipse projetée
Tracer le grand axe projeté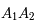 
Calculer l'excentricité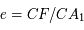 
, puis 
.
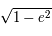Tracer le diamètre conjugu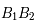é 
de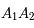 
(donc le projeté du petit axe).
Tracer point par point le projeté du cercle principal, par l'homothétie de l'ellipse projetée à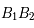 
et de rapport 
.
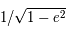La définition du cercle principal est donc:
Cercle principal d'une ellipse: Cercle de rayon a (demi grand axe de l'ellipse) de centre C
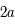du grand axe de l'orbite réelle.
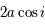où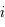 
est l'inclinaison du plan de l'orbite avec le plan de projection.
Mesurer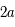 
sur ce grand axe, puis convertir cette valeur en UA (unité astronomique) connaissant l'échelle de la figure (longueur de la "flèche" correspond à 
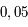seconde de degré) et la distance du Soleil au centre de la Galaxie (26 000 année-lumière)
Estimer la période du mouvement en utilisant les dates d'observations indiquées sur le tracé.
 |  |
et par l'image du foyer 
(c'est à dire la position indiquée de SgrA).
mm et 
mm
.
au milieu d'une corde parallèle à 
.
mm ce qui correspond à 
. Ce qui donne 
al 
ua.
ans. Donc 
est estimée à 
ans.
présente au foyer SgrA.
où 
est la vitesse angulaire (
), a le demi grand axe, M la masse et G une constante universelle (la constante de Gravitation).
correspond au Soleil.
et 
d'où 
an et 
ua, donc 
. Et donc 
masses solaires.