Théorème de Liouville

Auteurs: Stéphane Erard, Marc Fouchard

théorème de Liouville

Crédit : Astrophysique sur Mesure / Fouchard

Auteur : Marc Fouchard.

Le but de cet exercice est de montrer qu'un volume soumis à un flux, c'est-à-dire qu'en chaque point de l'espace on peut associer un vecteur vitesse donné par une équation différentielle d'ordre 1, hamiltonien reste constant.

La figure suivante illustre cette propriété dans le cas du problème de 2 corps plan. Comme on est à deux dimensions un volume correspond à une surface. Le disque est soumis à une force gravitationelle due à un corps massif se trouvant à l'origine. La surface verte est constante au cours du temps, même si la forme est fortement modifiée.

Un flux hamiltonien vérifie les équations d'hamilton. C'est-à-dire que le point de coordonnées 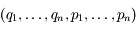$(q_1,\dots,q_n,p_1, \dots,p_n)$ vérifie les équations différentielles suivantes :

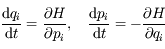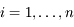$\frac{{\rm d}q_i}{{\rm d}t}=\frac{\partial H}{\partial p_i}, \quad \frac{{\rm d}p_i}{{\rm d}t}=-\frac{\partial H}{\partial q_i}$ , avec $i=1,\dots,n$ .

où 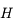est le hamiltonien du système, indépendant du temps.